МЕТОД ДИХОТОМИИ ВЫЧИСЛЕНИЯ КОРНЯ ФУНКЦИИНа интервале [ a, b ] задана непрерывная функция y = f (x), значения функции на концах интервала f (a) и f (b) имеют разные знаки. Требуется найти такое z, что | x 0 – z | ≤ ε / 2. Рекуррентная последовательность пар чисел { ui, vi }:
u:=a; v:=b; x:=(u+v)/2; while (v-u)>=eps do Begin if f(u)*f(x)<=0 then v:=x else u:=x; x:=(u+v)/2 End Трудоемкость: __________________________________________ Вычисление определенного интеграла I от функции f (x) на интервале [ a, b ] методом трапеций путем деления интервала на n равных частей.
________________________________________________________________
_________________________________________ type func=function(x:real):real; ___________________________________ function Integr(f:func; a,b:real;n:integer):real; var i:integer; d,s:real; begin s:=(f(a)+f(b))/2; d:=(b-a)/n; for i:=1 to n-1 do s:=s+f(a+i*d); Integr:=s*d End; _________________________________________ function f1(x:real):real; begin f1:=exp(sqrt(x)) end; ___________________________________ function f2(x:real):real; begin f2:=sqrt(exp(x)) end; ___________________________________ I1:=Integr(f1,0,1,10); вычисляет интеграл функции __________________________________________ I2:=Integr(f2,-1,1,20); вычисляет интеграл функции
|
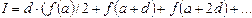
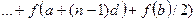
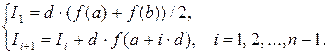
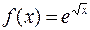на интервале [0,1] путем дробления интервала на 10 частей
на интервале [–1,1] путем дробления интервала на 20 частей.
