РЕКУРРЕНТНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Числовая последовательность { xk } называется рекуррентной ранга p, если
где a 0, a 1, …, ap – 1 – константы, а f – функция. __________________________________________ Сумма элементов ai – рекуррентная последовательность ранга 1:
__________________________________________ S:=0; for i:=1 to n do S:=S+ a (i); __________________________________________ Полином от x степени n можно представить в виде формулы Горнера:
где an, an –1, …, a 1, a 0 – коэффициенты полинома. Вычисление полинома при заданном значении x и коэффициентов a 0, a 1, …, an :
__________________________________________ P:=a[n]; for i:=1 to n do P:=P*x+a[n-i]; __________________________________________ Вычисление цифр a 0, a 1, …, an неотрицательного целого числа Pn при заданном значении основания x:
__________________________________________ i:=0; while P>0 do Begin a[i]:=P mod x; P:=P div x; i:=i+1 End; n:=i-1; __________________________________________ Числа Фибоначчи задаются рекуррентной последовательностью ранга 2:
__________________________________________ f1:=0; f2:=1; for k:=2 to n do Begin f3:=f2+f1; f1:=f2; f2:=f3 End __________________________________________
|





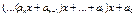 ,
,





