Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
21. Моменты инерции и радиусы инерции плоской фигуры.
Осевой момент инерции фигуры - этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:
Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:
Центробежный момент инерции фигуры - этоинтеграл произведений элементарных площадей на их расстояния до осей x и y:
Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4). Осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести поперечного сечения стержня, называют собственнымимоментами инерции.
Момент инерции фигуры относительно координатной оси может быть представлен в виде произведения площади фигуры на квадрат радиуса инерции:
Формула радиуса инерции имеет вид:
Главным центральным осям инерции соответствуют главные радиусы инерции:
Для прямоугольника (см. рис. 4.4, а) главные радиусы инерции равны:
Для круглого сечения формула главных радиусов инерции имеет вид:
23. Главные и центральные оси инерции. Определение угла наклона главных центральных осей.
Можно найти положение двух взаимно перпендикулярных осей, при котором Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ей перпендикулярна). Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями.
24. Виды расчетов на прочность.
|

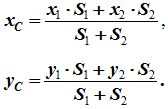


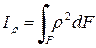
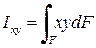
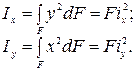
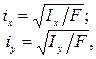
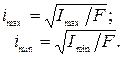
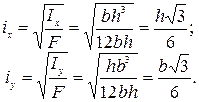
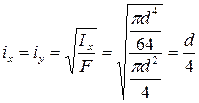
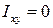 . Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).
. Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).


