ПРЕДЕЛЬНОЕ НАПРЯЖЕНИЕ В РАСЧЕТАХ НА ПРОЧНОСТЬ
В качестве предельного напряжения в расчетах на прочность принимается: предел текучести для пластичного материала (считается, что разрушение пластичного материала начинается при появлении в нем заметных пластических деформаций)
предел прочности для хрупкого материала, значение которого при растяжении и сжатии различно:
Для обеспечения прочности реальной детали необходимо так выбрать ее размеры и материал, чтобы возникающее в некоторой ее точке при эксплуатации наибольшеенормальное напряжение было меньше предельного:
Однако даже если наибольшеерасчетноенапряжение в детали будет близко к предельному напряжению, гарантировать ее прочность еще нельзя. внешние нагрузки действующие на деталь, не могут быть установлены достаточно точно, расчетные напряжения в детали могут быть вычислены иногда лишь приближенно, возможны отклонения действительных механических характеристик материала от расчетных характеристик. Деталь должна быть спроектирована с некоторым расчетным коэффициентом запаса прочности:
Ясно, что чем больше n, тем прочнее деталь. Однако очень большой коэффициент запаса прочности приводит к перерасходу материала, и это делает деталь тяжелой и неэкономичной. В зависимости от назначения конструкции устанавливается требуемый коэффициент запаса прочности Условие прочности: прочность детали считается обеспеченной, если
Отсюда можно получить и другую форму записи условия прочности:
Отношение, стоящее в правой части последнего неравенства, называют допускаемым напряжением:
Если предельные и, следовательно, допускаемые напряжения при растяжении и сжатии различны, их обозначают Тогда условие прочности при растяжении (сжатии) имеет вид:
Если расчетноенапряжение получается значительно ниже допускаемого напряжения, то материал расходуется нерационально. Допускается расчетное напряжение не более чем на 5 % превышающее допускаемое напряжение. Условие жесткости при растяжении и сжатии формула:
где
27. Напряженное состояние в точке тела.
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения. Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы В количественном выражении
Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K. Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении). Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши. Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( Между полным (
Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части. Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы: 1 МПа = 106 Па; 1 кН/см2 = 107 Па. В технической системе единиц напряжения измеряются в килограммах силы на миллиметр (сантиметр) в квадрате (кгс/мм2 или кгс/см2). Следует запомнить, что 1 кН/см2» 1 кгс/мм2.
|

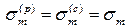 ,
,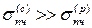 .
.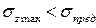
 .
. .
.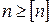 . Используя выражение
. Используя выражение 


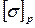 и
и 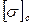 . Пользуясь понятием допускаемого напряжения, можно условие прочности сформулировать следующим образом: прочность детали обеспечена, если возникающее в ней наибольшее напряжение не превышает допускаемого напряжения.
. Пользуясь понятием допускаемого напряжения, можно условие прочности сформулировать следующим образом: прочность детали обеспечена, если возникающее в ней наибольшее напряжение не превышает допускаемого напряжения.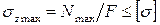
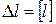
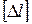 – допускаемое удлинение стержня.
– допускаемое удлинение стержня. , возникающей на бесконечно малой площадке
, возникающей на бесконечно малой площадке 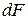 в окрестности данной точки (рис. 1.4, а).
в окрестности данной точки (рис. 1.4, а). .
.
 – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (
– сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (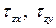 – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
– тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают. ), нормальным (
), нормальным (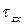 и
и 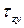 ) существует зависимость:
) существует зависимость: .
.


