НАГРУЗКИ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ
НАГРУЗКИ ПО СПОСОБУ ПРИЛОЖЕНИЯ По способу приложения нагрузки бывают объемными (собственный вес, силы инерции), действующими на каждый бесконечно малый элемент объема, и поверхностными. Поверхностные нагрузки делятся на сосредоточенные нагрузки и распределенные нагрузки. Распределенные нагрузки характеризуются давлением - отношением силы, действующей на элемент поверхности по нормали к ней, к площади данного элемента и выражаются в Международной системе единиц (СИ) в паскалях, мегапаскалях (1 ПА = 1 Н/м2; 1 МПа = 106 Па) и т.д., а в технической системе – в килограммах силы на квадратный миллиметр и т.д. (кгс/мм2, кгс/см2). В сопромате часто рассматриваются поверхностные нагрузки, распределенные по длине элемента конструкции. Такие нагрузки характеризуются интенсивностью, обозначаемой обычно q и выражаемой в ньютонах на метр (Н/м, кН/м) или в килограммах силы на метр (кгс/м, кгс/см) и т.д. НАГРУЗКИ ПО ХАРАКТЕРУ ИЗМЕНЕНИЯ ВО ВРЕМЕНИ По характеру изменения во времени выделяют статические нагрузки - нарастающие медленно от нуля до своего конечного значения и в дальнейшем не изменяющиеся; и динамические нагрузки вызывающие большие силы инерции.
4.Понятие о деформации. Упругие деформации. Остаточные деформации. Прочность. Жесткость.
Деформация – изменение взаимного расположения частиц тела, приводящее к изменению размеров и, обычно, формы тела. Полная деформация может состоять из упругой деформации и остаточной деформации. Упругая деформация исчезает после удаления внешней нагрузки, размеры и форма тела возвращаются к начальным значениям, остаточная (пластическая) деформация сохраняется после удаления нагрузки. Упругость – свойство тела получать упругую деформацию. Пластичность – свойство тела накапливать остаточную деформацию. Изотропность – свойство материала сохранять упругие свойства одинаковыми по всем направлениям. Если упругие свойства материала зависят от направлений, то такая особенность называется анизотропностью. Модуль упругости - это хар-ка сопротивления материалов упругой деформации. При достижении напряжениями так называемого предела упругости деформация становиться необратимой. Прочность – способность конструкции, а также ее частей и деталей выдерживать действие внешних нагрузок, не разрушаясь.
Жесткость – способность конструкции и ее элементов сопротивляться изменению своих первоначальных размеров и формы.
5.Напряженное состояние. Нормальные и касательные напряжения.
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения. Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы В количественном выражении
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении). Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши. Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( Между полным (
6. Основные виды деформаций и их характеристика.
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.
7. Реальный объект и расчетная схема.
Расчетная схема - это упрощенная, идеализированная схема, которая отражает наиболее существенные особенности объекта, определяющие его поведение под нагрузкой. Расчет реальной конструкции начинается с выбора расчетной схемы. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической формы реального объекта. Стержень – тело, длина которого существенно превышает характерные размеры поперечного сечения.
Брус – это тот же стержень.
Балка – стержень или брус, работающий на изгиб.
Пластина – тело, у которого толщина существенно меньше двух других размеров.
Оболочка – тело, ограниченное криволинейными поверхностями (искривленная пластина).
Массивное тело – элемент конструкции с размерами одного и того же порядка.
Ферма – стержневая конструкция, работающая только на растяжение или сжатие.
8. Внутренние силы. Метод сечения. Под действием внешней нагрузки любое реальное твердое тело изменяет свои размеры и форму, или деформируется, при этом порождая внутренние силы, противодействующие деформациям. Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить. Разрежем стержень, находящийся в равновесии под действием некоторой системы сил Отбросим одну из частей стержня и рассмотрим оставленную часть. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б
9. Напряжения и деформации при растяжении (сжатии). Закон Гука.
Растяжение (сжатие) - это вид деформации стержня, при котором происходит изменение его первоначальной длины. Растяжением (сжатием) называется такой вид деформации, когда в поперечном сечении стержня под действием внешних нагрузок возникает только один внутренний силовой фактор – продольная сила, а остальные внутренние силовые факторы отсутствуют.
Продольная сила вызывает нормальные напряжения, определяемые:
- при равномерном распределении их по сечению
- при неравномерном распределении
Продольная сила и напряжение положительны при растяжении и отрицательны при сжатии.
Для большинства конструкционных материалов между напряжением (
Закон Гука: Напряжение пропорционально деформации. Коэффициент пропорциональности (E) в формуле закона Гука I форма. В поперечных сечениях бруса при центральном растяжении (сжатии) нормальные напряжения равны отношению продольной силы к площади поперечного сечения: II форма. Относительная продольная деформация прямо пропорциональна нормальному напряжению, откуда.
10. Напряжения на косых площадках при растяжении. Напряжения в наклонных площадках наблюдаются, если мысленно «разрезать» стержень, растягиваемый силами P, наклонной плоскостью под углом
полное напряжение наклонного сечения в каждой точке будет равно:
где
11. Деформации при растяжении (сжатии). Абсолютное удлинение. Относительное удлинение (укорочение), коэффициент Пуассона
Пусть в результате деформации первоначальная длина стержня l станет равной. l 1. Изменение длины
называется абсолютным удлинением стержня. Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением (
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной. Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:
Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:
Для различных материалов коэффициентПуассона изменяется в пределах
15. Правила построения эпюр при растяжении (сжатии). Правило знаков. Контроль правильности построения эпюр.
Эпюра – график, показывающий изменение какого-либо параметра по длине конструкции. Эпюры дают наглядное представление о характере изменения силового фактора по длине или координате и позволяют установить местонахождение опасных сечений.
16. Экспериментальное определение механических характеристик при растяжении и сжатии.
Испытание на растяжение является наиболее распространенным видом испытания материалов, так как при нем наиболее ярко выявляются характеристики прочности и пластичности материалов. При статических испытаниях на растяжение определяются следующие основные механические характеристики материалов: предел пропорциональности – σпц; предел упругости – σу; предел текучести физический — σт; временное сопротивление – σв; относительное удлинение после разрыва – ε;; относительное сужение поперечного сечения после разрыва – ψ;; истинный предел прочности – σист;
|

 , возникающей на бесконечно малой площадке
, возникающей на бесконечно малой площадке 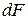 в окрестности данной точки (рис. 1.4, а).
в окрестности данной точки (рис. 1.4, а). .
. – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (
– сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения (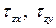 – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
– тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают. ), нормальным (
), нормальным (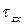 и
и 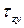 ) существует зависимость:
) существует зависимость: .
.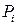 (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
(рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.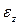 ) до определенного предела нагружения существует линейная зависимость
) до определенного предела нагружения существует линейная зависимость
 к поперечному сечению
к поперечному сечению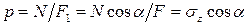
 – нормальное напряжение
– нормальное напряжение

 .
.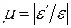
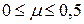 . Например, для пробки
. Например, для пробки 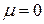 , для каучука
, для каучука  , для стали
, для стали  , для золота
, для золота 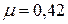 .
.


