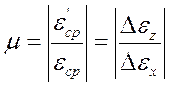Удельная работа, затраченная на разрыв – а.
Предел пропорциональности σпц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):
Предел упругости σу — напряжение, после которого появляется остаточное удлинение.В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу пропорциональности.
Затем криволинейная часть диаграммы переходит в почти горизонтальный участок — площадку текучести. Здесь деформации растут практически без увеличения нагрузки (участок ВС).
Эти линии представляет собой следы смещения отдельных частиц материала, обусловленного большими деформациями образца. Они называются линиями Чернова Предел текучести σт — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):
Временное сопротивление σв является основным показателем прочности материала и представляет собой наибольшее напряжение, которое выдерживает материал перед разрушением (МПа):
Относительное удлинение ε; — отношение абсолютного удлинения к первоначальной длине, выраженное в процентах:
Относительное суже ние ψ; — отношение уменьшения площади поперечного сечения образца после разрушения к первоначальной площади поперечного сечения, выраженное в процентах:
17. Основные механические характеристики материалов. Пластичные и хрупкие материалы. Явление наклепа.
Понятия предел прочности и временное сопротивление разрыву не являются тождественными. Предел прочности относится к случаю, когда образец разрушается без образования шейки, что характерно для хрупких материалов. Временное сопротивление разрыву относится к пластичным материалам.
Наклеп – изменение структуры и свойств металлического материала, вызванное пластической деформацией. Наклеп снижает пластичность и ударную вязкость, но увеличивает предел пропорциональность, предел текучести и твердость. Наклеп снижает сопротивление материала деформации противоположного знака. При поверхностном наклепе изменяется остаточное напряженное состояние в материале и повышается его усталостная прочность. Наклеп возникает при обработке металлов давлением (прокатка, волочение, ковка, штамповка), резанием, при обкатке роликами, при специальной обработке дробью. Повышение долговечности деталей машин методом поверхностного пластического деформирования (ППД) или поверхностного наклепа широко используется в промышленности для повышения сопротивляемости малоцикловой и многоцикловой усталости деталей машин. На рисунке 3 приведены схемы различных ППД.
18. Анализ диаграммы растяжения. Определение полной работы.
Прямолинейный участок диаграммы продолжается до некоторой точки А, за которой прекращается действие закона Гука. Нагрузка F пц, соответствующая точке А, служит для вычисления предела пропорциональности. Точка А (рис. 3) соответствует напряжению предела пропорциональности σпц. Предел пропорциональности σпц — наибольшее напряжение, до которого справедлив закон Гука, (МПа):
Площадь поперечного сечения образца на участке ОА практически не изменяется. Отсюда зона ОА именуется зоной упругости материала.
Предел упругости σу — напряжение, после которого появляется остаточное удлинение.В тех случаях, когда не требуется высокой точности, предел упругости принимается равным пределу пропорциональности. Затем криволинейная часть диаграммы переходит в почти горизонтальный участок — площадку текучести. Здесь деформации растут практически без увеличения нагрузки (участок ВС). Точка С соответствует пределу текучести σт. Предел текучести σт — наименьшее напряжение, при котором образец деформируется без увеличения нагрузки (МПа):
Зона ВС называется зоной общей текучести. На участке текучести ВС происходит существенная пластическая деформация
Временное сопротивление σв является основным показателем прочности материала и представляет собой наибольшее напряжение, которое выдерживает материал перед разрушением (МПа):
Зона CD называется зоной распределения. точка D на диаграмме соответствует напряжению предела прочности — временного сопротивления σв).
По диаграмме растяжения можно подсчитать работу, затраченную на разрыв образца. Она выражается площадью диаграммы, заключенной между кривой деформирования ОАВСDК (рис. 3) и осью абсцисс. Чем больше работа, затраченная на разрыв образца, тем больше энергии может поглотить образец без разрушения и тем лучше он будет сопротивляться ударным нагрузкам. Для получения величины, характеризующей не образец, а его материал, подсчитывается удельная работа разрыва а, т. е. количество работы, приходящееся на единицу объема образца:
19. Определение коэффициента Пуассона и модуля продольной упругости. Метод электротензометрирования. Диаграмма напряжений.
Определение коэффициента Пуассонаμ;. Коэффициентом поперечной деформации или коэффициентом Пуассона называется отношение относительной поперечной деформации образца при растяжении (сжатии) ε;' к относительной продольной деформации ε;,найденных в пределах пропорциональности:
Это отношение для каждого материала, в пределах упругости является величиной постоянной – упругой константой. Для определения коэффициента поперечной деформации необходимо подвергнуть образец растяжению (или сжатию) в пределах пропорциональности, с измерениями продольных и поперечных его деформаций.
Испытание производится на образце прямоугольного поперечного сечения, который описан и использован при опытном определении модуля упругости Е. Там же указывалась методика нахождения продольных деформаций такого образца. Для измерения поперечных деформаций при нагружении образца в соответствующем его направлении наклеиваются тензорезисторы. Их необходимо также располагать попарно на противоположных плоскостях образца (рис. 4) с целью устранения влияния возможного малого его искривления и возможной внецентренности приложения нагрузки. При такой установке тензорезисторов можно, найдя поперечные деформации образца на противоположных плоскостях, привести их к деформации его по средней плоскости, взяв среднее арифметическое соответствующих деформаций, т.е.
где ε'2, ε'3 – относительные поперечные деформации на противоположных плоскостях образца, полученные по показаниям тензорезисторов Т2 и ТЗ (рис. 4); ε' – относительная поперечная деформация в средней плоскости испытываемого образца. По усредненному значению продольных εср и поперечных ε'ср деформаций, соответствующих интервалу нагружения образца, подсчитывается коэффициент Пуассона (3):
20. Геометрические характеристики плоских сечений. Статический момент. Определение центра тяжести плоской фигуры.
При расчетах элементов конструкций используются различные геометрические характеристики, а именно: 1) Площадь поперечного сечения (см2, мм2). 2) Статические моменты сечения (см3, мм3). 3) Осевые моменты инерции сечения (см4, мм4). 4) Полярные моменты инерции сечения (см4, мм4). 5) Центробежные моменты инерции (см4, мм4). 6) Осевые и полярные моменты сопротивления сечения (см3, мм3). Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):
|


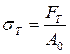

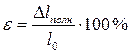 (6)
(6)


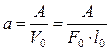
 (3)
(3)