Деление отрезка в данном отношении
Теги: вектор, координатная плоскость, лекция по высшей математики, деление отрезка, высшая математика |
Пусть даны точки A(x1;y1) и B(x2;y2).
Координаты точки М(х,у), лежащей на отрезке АВ и делящей его в данном отношении:
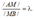 вычисляются по формулам:
 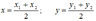 В частности, при  получаются формулы для координат середины отрезка: получаются формулы для координат середины отрезка:
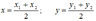 Пример 2. Известны точки A(-2;5), B(4;17)- концы отрезка [AB]. На этом отрезке находится точка М, расстояние которой от А в два раза больше расстояния от В. Определить координаты точки М.
Решение. Так как |AM|=2|MB|, то 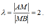 . Здесь x1=-2, y1=5, x2=4, y2=17; следовательно, . Здесь x1=-2, y1=5, x2=4, y2=17; следовательно,  то есть M(2;13). то есть M(2;13).
Пример 3. Точка M(2;3) служит серединой отрезка [AB]. Определить координаты точки А, если B(7;5).
Решение. Здесь x=2, y=3, x2=7, y2=5, откуда
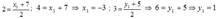 то есть A(-3;1)
|
Изобразим в прямоугольной декартовой системе координат некоторый отрезок АВ, точку С на нем и построим радиус-векторы точек А, В и С, а также векторы  и
и  . Будем считать, что точка С делит отрезок АВ в отношении
. Будем считать, что точка С делит отрезок АВ в отношении  .
.
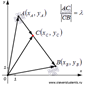
Мы знаем, что координаты радиус-вектора точки равны соответствующим координатам этой точки, поэтому,  и
и  . Найдем координаты вектора
. Найдем координаты вектора  , которые будут равны искомым координатам точки С, делящей отрезок АВ в заданном отношении
, которые будут равны искомым координатам точки С, делящей отрезок АВ в заданном отношении  .
.
В силу операции сложения векторов можно записать равенства  и
и  . Их мы используем в следующем абзаце.
. Их мы используем в следующем абзаце.
Так как точка С делит отрезок АВ в соотношении  , то
, то  , откуда
, откуда  . Векторы
. Векторы  и
и  лежат на одной прямой и имеют одинаковое направление, а выше мы отметили, что
лежат на одной прямой и имеют одинаковое направление, а выше мы отметили, что 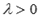 , поэтому, по
, поэтому, по определению операции умножения вектора на число справедливо равенство  . Подставив в него
. Подставив в него  , имеем
, имеем 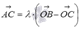 . Тогда равенство
. Тогда равенство  можно переписать как
можно переписать как  , откуда в силу
, откуда в силу свойств операций над векторами получаем  .
.
Осталось вычислить координаты вектора 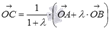 , выполнив необходимые
, выполнив необходимыеоперации над векторами 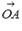
и 
в координатах. Так как  и
и 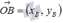 , то
, то  , следовательно,
, следовательно,  .
.
Таким образом, на плоскости координаты точки С, которая делит отрезок АВ в отношении  , находятся по формулам
, находятся по формулам  и
и  .
.