Идентификация объекта управления
Под идентификацией объектов понимается построение их математических моделей в результате статистической обработки экспериментальных данных, полученных при функционировании объекта. Если априорная информация об идентифицируемом объекте позволила выбрать структуру модели (общий вид математических соотношений, связывающих входы и выходы) и задача идентификации состоит в определении параметров модели (коэффициентов усиления, постоянных времени и т.п.), то задачу идентификации называют задачей идентификации в узком смысле или оцениванием параметров. Если же и структуру, и параметры модели предстоит установить в процессе идентификации, то речь идет об идентификации в широком смысле слова. В дальнейшем, говоря об идентификации, будем иметь в виду оценивание параметров. Одним из наиболее распространенных методов идентификации является метод наименьших квадратов (МНК), предложенный К. Гауссом. В данном разделе разработается для каждого из возможных вариантов структуры объекта программы, моделирующие изменение выхода объекта yм(i) при известном входном сигнале u(i). При одном и том же u(i) последовательность yм(i) зависит от вектора параметров А модели объекта. В состав вектора А входят коэффициент усиления К и постоянные времени Тj модели объекта. Имея значения u(i), y(0) и вектор A параметров объекта, можно рассчитать модельное значение выхода yM(i). В общем случае yM(i) ≠ y(i), так как модель всегда лишь приближённо отражает свойства реального объекта. Кроме того, отклонение модельного значения выхода от экспериментального может быть вызвано разной структурой модели и вектора параметров A. В процессе идентификации объекта вектор A стремятся выбрать так, чтобы последовательность yM(i) была как можно ближе к экспериментальным значениям y(i). В качестве меры близости (критерия идентификации) чаще всего выбирают функционал F, представляющий собой сумму квадратов разностей (невязок) между модельными и наблюдаемыми значениями
N – дискретное время моделирования. При этом в качестве оценки неизвестных параметров A объекта целесообразно выбирать значение Процедура идентификации выполняется для каждого возможного варианта структуры объекта. В качестве модели объекта окончательно принимается та структура и тот набор параметров А, которые обеспечивают после минимизации наименьшее значение F. Рассмотрим обе модели.
Модель 1.
Рис.2.1 Схема для 1-ой модели
Рис.2.2 Графики y(t), и ym(t) до оптимизации параметров F=82.34, K=1, T1=1, T2=1.
Рис.2.3 Графики y(t), и ym(t) после оптимизации параметров F=0.005026 K=1.2748, T1=12.1222, T2=8.6656.
Рис.2.4 Графики y(t), и ym(t) до оптимизации параметров F=3427 K=10, T1=10, T2=10.
Рис.2.5 Графики y(t), и ym(t) после оптимизации параметров F=0.002955 K=1.2694, T1=12.0704, T2=8.5388.
Рис.2.6 Графики y(t), и ym(t) до оптимизации параметров F=1056 K=15, T1=2, T2=7.
Рис.2.7 Графики y(t), и ym(t) после оптимизации параметров F=0.001376 K=1.2673, T1=12.4740, T2=8.5474.
Модель 2.
Рис.2.8 Схема для 2-ой модели
F=40.79 K=1, T1=1, T2=1.
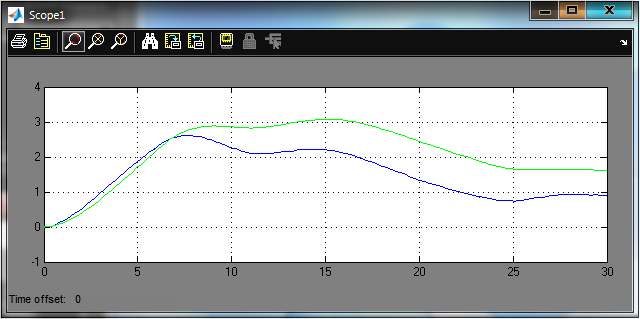
Рис.2.10 Графики y(t), и ym(t) после оптимизации параметров F=0.21226 K=1.1969, T1=3.8161, T2=3.8161.
Рис.2.11 Графики y(t), и ym(t) до оптимизации параметров F=17.03 K=2, T1=10, T2=3.
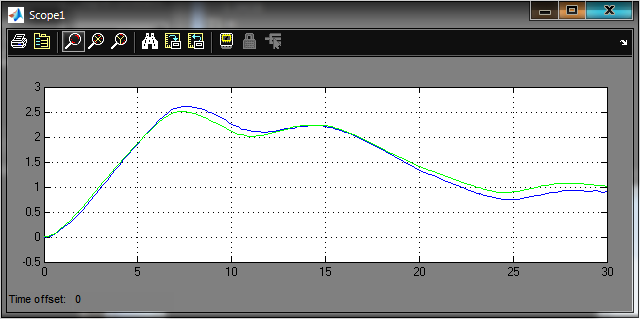
Рис.2.12 Графики y(t), и ym(t) после оптимизации параметров F=0.2509 K=1.3388, T1=8.5928, T2=1.2483.
Рис.2.13 Графики y(t), и ym(t) до оптимизации параметров F=324.2 K=5, T1=7, T2=12.
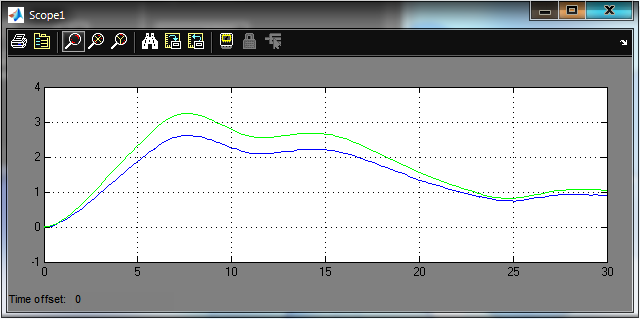
Рис.2.14 Графики y(t), и ym(t) после оптимизации параметров F=0.2789 K=1.3458, T1=1.1887, T2=8.7090.
Рис.2.15 Графики y(t), и ym(t) до оптимизации параметров F=3.744 K=1.5, T1=2, T2=6.
Рис.2.16 Графики y(t), и ym(t) после оптимизации параметров F=0.03135 K=1.2367, T1=2.0893, T2=6.0743.
После проведения оптимизации получил значения функционалов и коэффициентов моделей объекта. Модель 1: Для проведения моделирования объекта рациональнее выбрать первую модель, так как у нее меньший критерий идентификации, то есть модель будет выглядеть: Заключение В курсовом проекте моделировал работа контура регулирования. В первой части выполнили моделирование посредством программы Matlab и Simulink. Получили последовательности значений управляющего сигнала u(t) с выхода регулятора и выходного сигнала контура y(t). Построилb графики этих сигналов. Во второй части проекта идентифицировали две структуры объекта, пытаясь найти их параметры через найденные последовательности сигналов u(t) и y(t). В итоге, в результате идентификации объекта управления выяснили, что объект управления лучше аппроксимирует передаточная функция
|

 (2.1)
(2.1) , минимизирующее F:
, минимизирующее F: 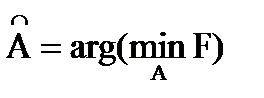 . Полученная таким образом оценка A называется оценкой метода наименьших квадратов (МНК–оценкой).
. Полученная таким образом оценка A называется оценкой метода наименьших квадратов (МНК–оценкой).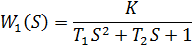

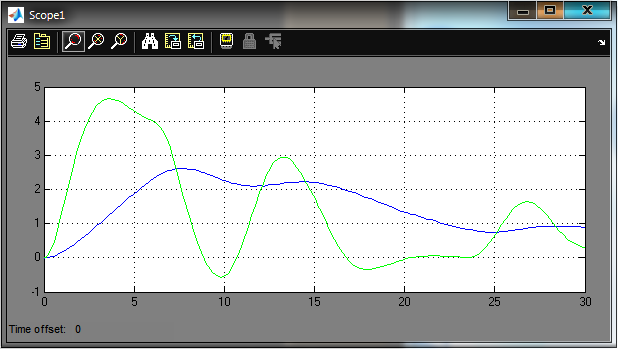
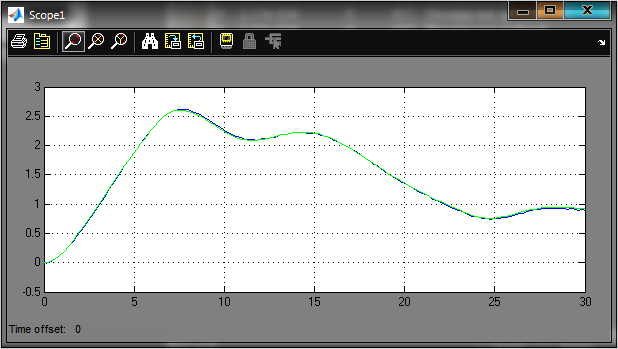
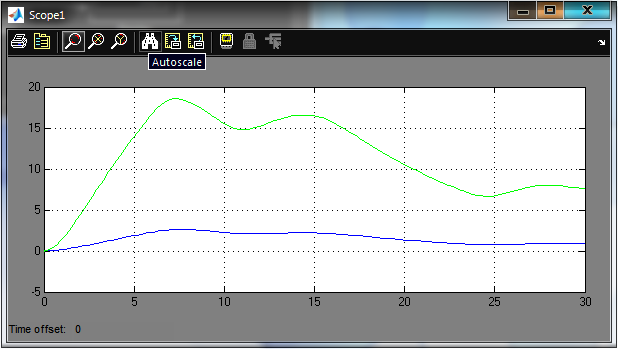
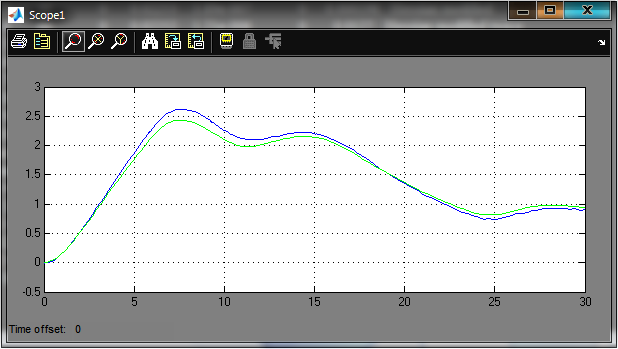

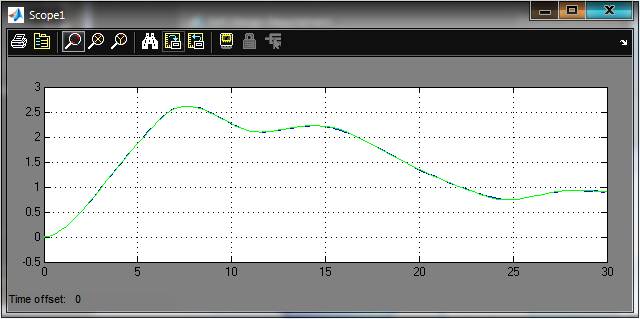

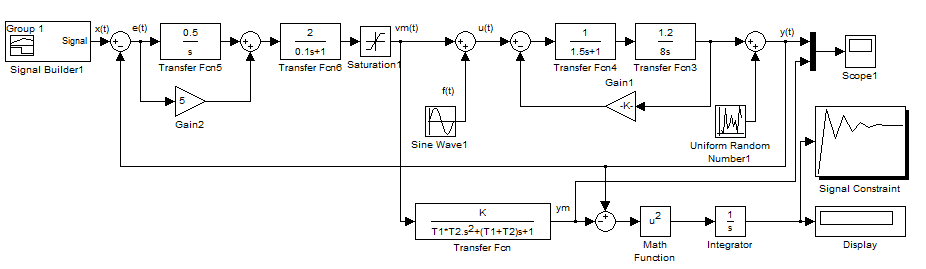
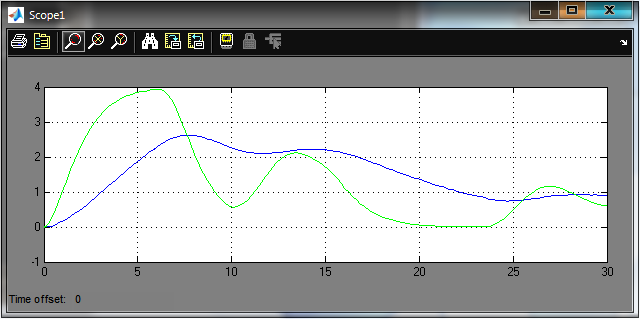 Рис.2.9 Графики y(t), и ym(t) до оптимизации параметров
Рис.2.9 Графики y(t), и ym(t) до оптимизации параметров



 имеет наименьшее значение функционала F=0.01376 с коэффициентами K=1.2673, T1=12.4740, T2=8.5474. Модель 2:
имеет наименьшее значение функционала F=0.01376 с коэффициентами K=1.2673, T1=12.4740, T2=8.5474. Модель 2:  имеет наименьшее значение функционала F=0.03135 с коэффициентами K=1.2367, T1=2.0893, T2=6.0743.
имеет наименьшее значение функционала F=0.03135 с коэффициентами K=1.2367, T1=2.0893, T2=6.0743.
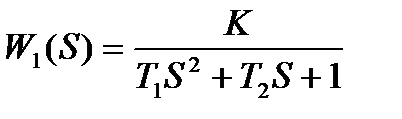 , так как она после минимизации обеспечивает наименьшее значение функционала F=0.001376.
, так как она после минимизации обеспечивает наименьшее значение функционала F=0.001376.


