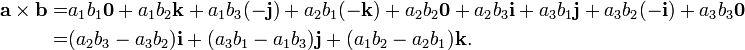Edit]Coordinate notation
Standard basis vectors (i, j, k, also denoted e 1, e 2, e 3) and vector components of a (a x, a y, a z, also denoted a 1, a 2, a 3) The standard basis vectors i, j, and k satisfy the following equalities:
which imply, by theanticommutativity of the cross product, that
The definition of the cross product also implies that
These equalities, together with the distributivity and linearity of the cross product, are sufficient to determine the cross product of any two vectors a and b. Each vector can be defined as the sum of three orthogonal components parallel to the standard basis vectors:
Their cross product a × b can be expanded using distributivity:
This can be interpreted as the decomposition of a × b into the sum of nine simpler cross products involving vectors aligned with i, j, or k. Each one of these nine cross products operates on two vectors that are easy to handle as they are either parallel or orthogonal to each other. From this decomposition, by using the above mentioned equalities and collecting similar terms, we obtain:
meaning that the three scalar components of the resulting vector c = c 1 i + c 2 j + c 3 k = a × b are
Using column vectors, we can represent the same result as follows:
|



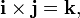


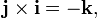
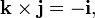
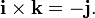
 (the zero vector).
(the zero vector).