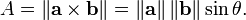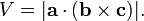Edit]Geometric meaning
See also: Triple product
Figure 1. The area of a parallelogram as a cross product
Figure 2. Three vectors defining a parallelepiped The magnitude of the cross product can be interpreted as the positive area of theparallelogram having a and b as sides (see Figure 1):
Indeed, one can also compute the volume V of a parallelepiped having a, b and c as sides by using a combination of a cross product and a dot product, called scalar triple product(see Figure 2):
Since the result of the scalar triple product may be negative, the volume of the parallelepiped is given by its absolute value. For instance,
Because the magnitude of the cross product goes by the sine of the angle between its arguments, the cross product can be thought of as a measure of "perpendicularness" in the same way that the dot product is a measure of "parallelness". Given two unit vectors, their cross product has a magnitude of 1 if the two are perpendicular and a magnitude of zero if the two are parallel. The opposite is true for the dot product of two unit vectors. Unit vectors enable two convenient identities: the dot product of two unit vectors yields the cosine (which may be positive or negative) of the angle between the two unit vectors. The magnitude of the cross product of the two unit vectors yields the sine (which will always be positive).
|