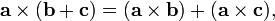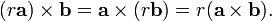edit]Algebraic properties
The cross product is anticommutative,
distributive over addition,
and compatible with scalar multiplication so that
It is not associative, but satisfies the Jacobi identity:
Distributivity, linearity and Jacobi identity show that R 3 together with vector addition and the cross product forms a Lie algebra, the Lie algebra of the real orthogonal group in 3 dimensions, SO(3). The cross product does not obey the cancellation law: a × b = a × c with non-zero a does not imply that b = c. Instead if a × b = a × c:
If neither a nor b - c is zero then from the definition of the cross product the angle between them must be zero and they must be parallel. They are related by a scale factor, so one of b or c can be expressed in terms of the other, for example
|