Нестационарный режим работы. Условие самовозбуждения
Для проведения дальнейших рассуждений заметим, что в начальный момент после включения генератора амплитуды колебаний будут малыми, поэтому на этом малом промежутке времени будем рассматривать генератор как линейное устройство. На большие интервалы времени это допущение не распространяется, потому что амплитуды автоколебаний возрастают настолько, что систему уже нельзя считать линейной. Задача состоит в следующем: необходимо найти условие. При котором процесс на выходе будет нарастающим. Рассмотрим решение задачи для простейшего автогенератора на полевом транзисторе с трансформаторной обратной связью (рисунок 2.2). Для упрощения задачи рассмотрим эквивалентную схему (рисунок 2.3) Используя схему замещения, составляем уравнение по первому закону Кирхгоффа
Зная компонентное уравнение индуктивности, можно записать следующее выражение:
Выразим все токи через
Так как
то
Подставляя выражения (2.10), (2.11), (2.12) и (2.14) в уравнение (2.8), получим следующее уравнение:
Введём обозначения
Подставим (2.17) и (2.18) в уравнение (2.16), получим дифференциальное уравнение, описывающее переходной процесс после включения генератора.
Характеристическое уравнение, соответствующее уравнению (2.19) выглядит следующим образом:
очевидно, что
где В случае комплексно-сопряженных корней решение уравнения (2.19) записывается в следующем виде:
При различных значениях a)
b)
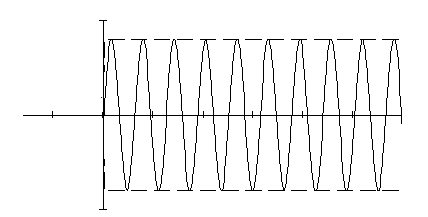
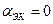
c)
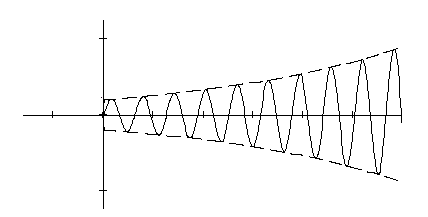
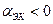
Таким образом можно сделать вывод о том, что для автогенерации необходимо выполнение условия:
При малых амплитудах процесс будет нарастать, однако до бесконечности этого происходить не будет, так как при больших амплитудах устройство уже нельзя считать линейным, и данная модель уже не будет работать. Подставляем (2.18) в (2.24)
Учитывая, что
откуда
Выражение (2.29) и есть условие возбуждения автогенератора. Кольцевое усиление сразу после включения питания должно быть больше единицы.
|

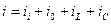

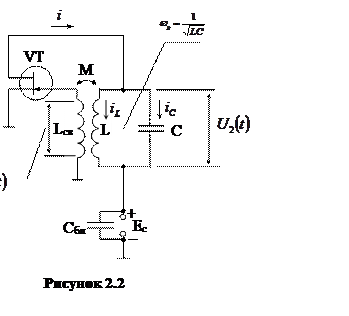 . (2.8)
. (2.8)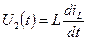 . (2.9)
. (2.9)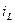 :
: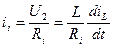 , (2.10)
, (2.10)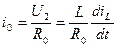 , (2.11)
, (2.11) . (2.12)
. (2.12)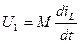 , (2.13)
, (2.13) . (2.14)
. (2.14) , (2.15)
, (2.15)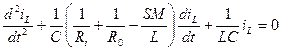 . (2.16)
. (2.16)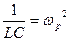 , (2.17)
, (2.17) . (2.18)
. (2.18)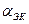 - эквивалентный коэффициент затухания. Учитываем как затухание в контуре, вызванное
- эквивалентный коэффициент затухания. Учитываем как затухание в контуре, вызванное 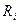 и
и  - со знаком +, так и влияние обратной связи со знаком минус – отрицательное затухание.
- со знаком +, так и влияние обратной связи со знаком минус – отрицательное затухание. 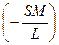 , что эквивалентно внесению отрицательной проводимости в контур. За счёт ПОС получаем компенсацию активных потерь в контуре.
, что эквивалентно внесению отрицательной проводимости в контур. За счёт ПОС получаем компенсацию активных потерь в контуре. . (2.19)
. (2.19)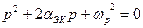 , (2.20)
, (2.20) , (2.21)
, (2.21) , поэтому
, поэтому , (2.22)
, (2.22)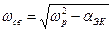 .
. . (2.23)
. (2.23)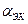 процесс будет иметь различный вид:
процесс будет иметь различный вид: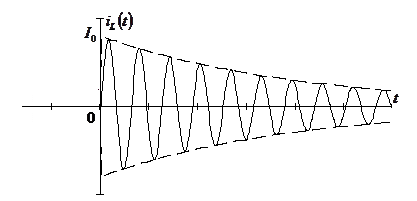 при
при 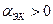
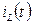
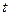
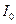

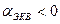 . (2.24)
. (2.24) , (2.25)
, (2.25) , (2.26)
, (2.26) . (2.27)
. (2.27)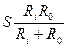 - коэффициент усиления транзистора на резонансной частоте
- коэффициент усиления транзистора на резонансной частоте 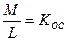 – коэффициент передачи цепи ОС, то неравенство (2.27) можно записать в несколько ином виде:
– коэффициент передачи цепи ОС, то неравенство (2.27) можно записать в несколько ином виде: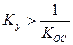 , (2.28)
, (2.28) . (2.29)
. (2.29)


