РЕФЕРАТ
Выбор в условиях нечеткой неопределенности
Выполнил ст. гр. ИОТ-818 С.В.Гребень
Руководитель В.Е. Бахрушин
2012 г. Целью данной работы является описание процесса выбора в условиях нечеткой неопределенности, особенностей задач принятия решений и рассмотрении на примере одного из видов задач.
Задание 2 Вступление 4 1 Сущность нечетких множеств 5 2 Задачи достижения нечеткой цели 6 2.1 Теоретическая часть 6 2.2 Пример 7 Выводы 9 Список литературы 10
ВСТУПЛЕНИЕ Язык нечетких множеств имеет существенные преимущества перед языком теории вероятностей в том случае, когда оценки получаются из опроса экспертов. Известно, что люди в большинстве своем неправильно оценивают вероятности (особенно большие и малые). Потому требовать от экспертов – специалистов в конкретных предметных областях, а не математиков, оценок в форме распределения вероятности зачастую невозможно8. Использование же полученных результатов для принятия решений можно квалифицировать как самонадеянное. Описание в форме нечетких множеств гораздо менее требовательно к квалификации экспертов и зачастую гораздо точнее отражает суть дела и имеющуюся у ЛПР информацию. Конечно, за это удобство приходится платить. Предлагаемые теорией решения, основанные на нечеткой информации, и сами несут на себе печать нечеткости. Они могут рассматриваться лишь как рекомендации для ЛПР, требуя от него выбора одного из предлагаемых вариантов. Тем не менее, даже этот факт можно рассматривать как достоинство теории – он показывает, как увеличение информированности ЛПР сказывается на достоверности и правильности принимаемых решений.
1 СУЩНОСТЬ НЕЧЕТКИХ МНОЖЕСТВ
В математике давно используется понятие множества – совокупности объектов, выделенных по некоторому признаку. Это понятие является базовым в современной математике и потому не определяется строго, формально. Так, если задано некоторое базовое множество X (конечное или бесконечное), то его подмножеством (четким подмножеством) A называется любое множество, содержащее в себе только элементы множества X (хотя, может быть, и не все его элементы). В четком множестве любой элемент может или принадлежать ему, или не принадлежать, поэтому функция принадлежности принимает лишь два возможных значения – ноль или единица. В нечетком же множестве (точнее, в нечетком подмножестве базового множестваX) любой элемент x ∈ X может принадлежать множеству с некоторой степенью достоверности, принимающей значения от нуля (элемент достоверно не принадлежит множеству) до единицы (элемент достоверно принадлежит множеству). Соответственно и функция принадлежности нечеткого множества может принимать любое значение из отрезка [0; 1].
2 ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЙ ПРИ НЕЧЕТКОЙ НЕОПРЕДЕЛЕНОСТИ
2.1 Задача достижения нечеткой цели Итак, мы обобщили на нечеткий случай понятия отображения, образа и прообраза множеств. Этого нам хватит для того, чтобы сформулировать и решить простейшую задачу принятия решения в условиях нечеткой информации. Задача формулируется так. Есть множество X возможных действий ЛПР и множество Y состояний управляемой системы. ЛПР в различной степени устраивают различные состояния системы – он стремится достичь своей цели, задаваемой нечетким подмножеством Задача ЛПР состоит в том, чтобы определить действие (возможно, нечеткое), которое позволило бы ему одновременно достичь цели Предположим, что отображение
2.2 Пример: Рассмотрим задачу, с которой периодически сталкивается каждый студент – задачу подготовки к экзамену. Пусть множество X = {1; 2; 3; 4; 5} задает возможные уровни подготовки к экзамену (большее значение соответствует более интенсивной подготовке), а множество Y = {1; 2; 3; 4; 5} описывает возможные исходы экзамена (оценки). Пусть студента одинаково устраивает как оценка 4, так и 5 (наш студент не гонится за отличной оценкой), но категорически не устраивают оценки 1 или 2. Оценка 3 студента устраивает лишь частично. Тогда цель студента можно описать нечетким множеством
В то же время (в связи с недостатком времени или способностей) студент ограничен в возможностях подготовки к экзамену, и если возможность подготовки на уровне 1 и 2 не вызывает сомнений, то большие уровни подготовленности уже более сомнительны. В следующей таблице приведена функция принадлежности нечеткого множества ограничений
Предположим, что отображение, переводящее действия в результат, тождественное, то есть уровень подготовки однозначно определяет оценку на экзамене – уровень подготовки 1 приводит к оценке 1, уровень подготовки 2 – к оценке 2 и так далее. Тогда задача выбора действия, достигающего цели с учетом ограничений, сводится к нахождению пересечения
Но ведь в реальности то принимается единственное решение! И отдельного рассмотрения требует вопрос о конкретном действии, выбираемом на основе нечеткой рекомендации. · Часто в качестве четкого решения задачи достижения нечеткой цели предлагается выбор действия, имеющего максимальную степень принадлежности нечеткому решению – множеству
ВЫВОДЫ Я рассмотрел в своей работе задачу достижения нечеткой цели с примером. Существует множество различных видов задач выбора в условиях нечеткой информации, в которых функции принадлежности могут иметь самый разный смысл. В то же время, у них есть одна общая черта - решение, предлагаемое ими также имеет некоторую нечеткость, предлагая ЛПР несколько вариантов выбора,
СПИСОК ЛИТЕРАТУРЫ
1. 1. Новиков Д.А., Петраков С.Н. Курс теории активных систем. М.: СИНТЕГ, 1999. 2. Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. – М.: Наука. 1981. 3. Беллман Р., Задэ Л. Принятие решений в расплывчатых условиях. -В кн.: Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. с.172 - 215. 4. Интернет -ресурс www.ru.wikipedia.org
|

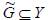 . Для достижения своей цели центр выбирает действия так, чтобы удовлетворить ограничениям на действия, задаваемым нечетким подмножеством
. Для достижения своей цели центр выбирает действия так, чтобы удовлетворить ограничениям на действия, задаваемым нечетким подмножеством  . Состояние, в которое переходит система в зависимости от действия ЛПР, описывается нечетким отображением
. Состояние, в которое переходит система в зависимости от действия ЛПР, описывается нечетким отображением 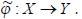 .
.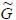 и удовлетворить ограничениям
и удовлетворить ограничениям 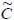 .
.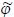 – тождественное, и множество действий совпадает с множеством результатов. В этом случае и цель и ограничения являются подмножествами одного и того же множества X, а нечеткое множество
– тождественное, и множество действий совпадает с множеством результатов. В этом случае и цель и ограничения являются подмножествами одного и того же множества X, а нечеткое множество 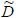 действий, которые одновременно и достигают цели, и удовлетворяют ограничениям, равно пересечению нечетких множеств цели и ограничений,
действий, которые одновременно и достигают цели, и удовлетворяют ограничениям, равно пересечению нечетких множеств цели и ограничений, 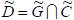 . Тогда множество
. Тогда множество 

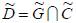 множеств цели и ограничений. Функция принадлежности множества
множеств цели и ограничений. Функция принадлежности множества  Таким образом, решение задачи достижения нечеткой цели само оказывается нечетким. Эта нечеткость является прямым следствием нечеткости в постановке задачи и может интерпретироваться как нечеткая рекомендация вида «готовиться примерно на 4».
Таким образом, решение задачи достижения нечеткой цели само оказывается нечетким. Эта нечеткость является прямым следствием нечеткости в постановке задачи и может интерпретироваться как нечеткая рекомендация вида «готовиться примерно на 4».


