ЗАДАЧА 4. Плоская задача теории упругости
Условие. Упругое тело заданной формы находится в условиях плоской задачи. Схема задачи и нагрузка даны на рис. 4.1 в соответствии с номером варианта.
Требуется: 5. Проверить, является ли заданная функция напряжений решением плоской задачи теории упругости. 6. Найти выражения для напряжений. 7. Составить граничные условия и найти постоянные, входящие в выражения для напряжений. 8. Проверить, удовлетворяют ли окончательные выражения для напряжений дифференциальным уравнением равновесия. 9. Построить эпюры напряжений в характерных сечениях.
Для упругого полубесконечного массива, находящегося в условиях плоской задачи (плоская деформация) под действием равномерно распределенной нагрузки (рис. 4.2) функция напряжений задана в виде
1. Вычисляются производные от функции напряжений:
Рис. 4.1. Схемы к задаче 4
Рис. 4.1. Схемы к задаче 4 (продолжение)
Рис. 4.1. Схемы к задаче 4 (окончание)
Рис. 4.2. Бигармоническое уравнение записывается в развернутом виде с учетом полученных выражений для вторых производных:
Подстановка полученных соотношений в бигармоническое уравнение обращает его в тождество
Следовательно, заданная функция напряжений является решением плоской задачи.
2. Записываются выражения для напряжений. С учетом отсутствия объемных сил
окончательно
3. Из граничных условий определяются постоянные A, B, C, D.
а) Горизонтальная грань. Геометрическое уравнение грани
проекции нагрузки на координатные оси
после подстановки формул для напряжений с учетом уравнения грани
б) Наклонная грань. Геометрическое уравнение грани
нагрузки
Совместное решение четырех уравнений дает выражения для постоянных
Выражения для напряжений после подстановки постоянных принимают окончательный вид:
4. Для проверки полученные выражения для напряжений подставляются в дифференциальные уравнения равновесия
В рассматриваемом примере проекции объемных сил на координатные оси
Подстановка производных показывает, что дифференциальные уравнения равновесия удовлетворяются тождественно.
5. Характерным сечением в данной задаче является горизонтальное сечение
При этом из схемы задачи следует, что Для построения эпюр напряжений необходимо задаваться числовыми значениями величины
При
Рис. 4.3. Плоская задача теории упругости Выполним проверку статических граничных условий на грани
Проекции сил, действующих на гранях материальной точки, на координатные оси
следовательно материальная точка находится в равновесии и эпюры напряжений построены верно.
|


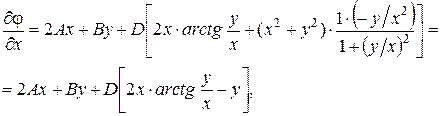
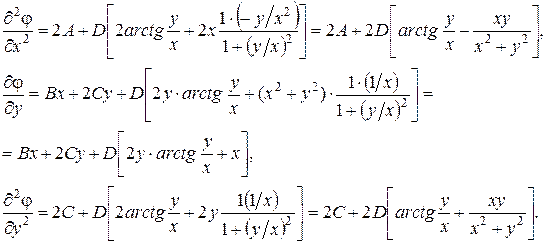

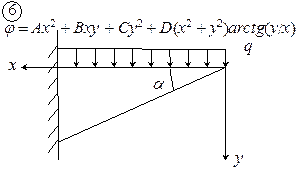
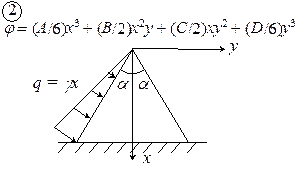

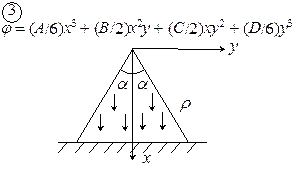
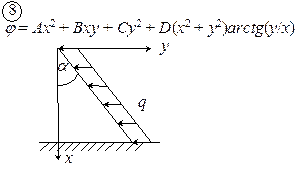


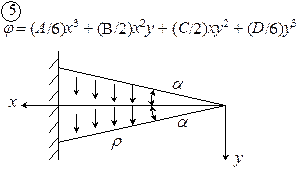
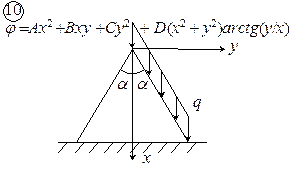






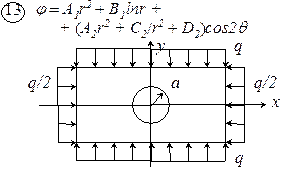


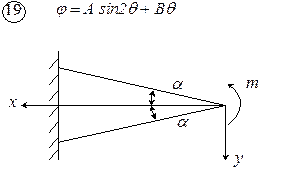



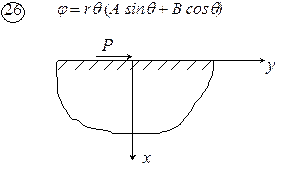
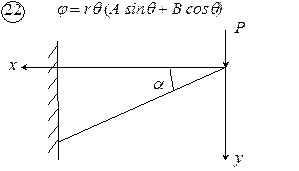


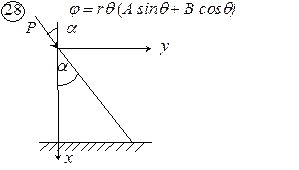

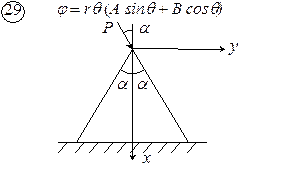

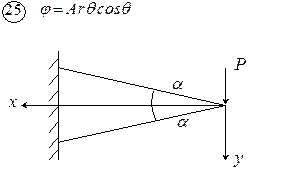





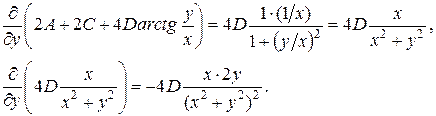
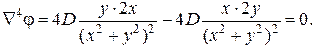

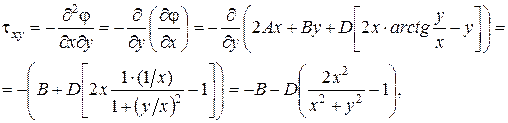
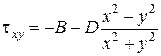 .
. . Для этой грани направляющие косинусы
. Для этой грани направляющие косинусы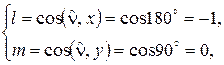
 (рис 4.3). Статические граничные условия
(рис 4.3). Статические граничные условия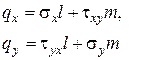
 принимают вид:
принимают вид: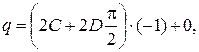 (1)
(1) (2)
(2)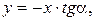
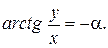 Направляющие косинусы
Направляющие косинусы
 Аналогично горизонтальной грани записываются два уравнения:
Аналогично горизонтальной грани записываются два уравнения: (3)
(3) (4)
(4)


 , производные
, производные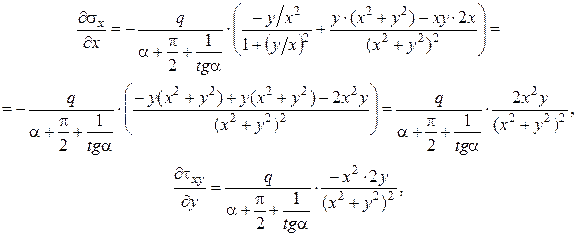

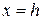 (рис. 4.3). После подстановки этого значения в формулы для напряжений получаются соотношения для построения эпюр:
(рис. 4.3). После подстановки этого значения в формулы для напряжений получаются соотношения для построения эпюр:
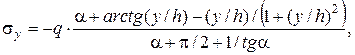
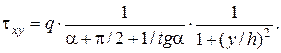
 .
. На рис. 4.3 показаны эпюры напряжений, построенные при
На рис. 4.3 показаны эпюры напряжений, построенные при  по точкам
по точкам  При этом в формулы угол
При этом в формулы угол 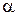 нужно подставлять в радианах. Для более точного выявления очертания эпюр необходимо брать точки чаще.
нужно подставлять в радианах. Для более точного выявления очертания эпюр необходимо брать точки чаще. ,
,  ,
, 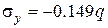 ,
, 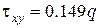 ;
;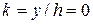 ,
, 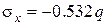 ,
, 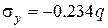 ,
, 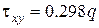 ;
;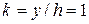 ,
,  ,
, 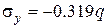 ,
, 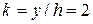 ,
, 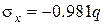 ,
,  ,
,  .
.
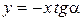 . Для этого рассмотрим дифференциально малый элемент тела, находящийся на поверхности в сечении
. Для этого рассмотрим дифференциально малый элемент тела, находящийся на поверхности в сечении 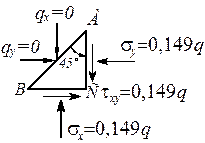

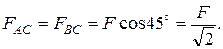
 ,
,  ,
,


