Тема: Обработка двумерных массивов.
Цель: Приобретение навыков составления алгоритмов и программ, использующих вложенные циклы
При выполнении данной работы используется материал предыдущей лабораторной работы. Поскольку обработка многомерных массивов (матриц) требует написания программ, в которых циклы вложены один в другой, необходимо знать правило вложения циклов: внешний цикл должен целиком охватывать все внутренние циклы; количество внутренних циклов и глубина вложений теоретически не ограничиваются, и определяются возможностями конкретной вычислительной системы (объемом оперативной памяти ЭВМ и версией компилятора).
В условиях заданий СА обозначает среднее арифметическое, СГ – среднее геометрическое.
Варианты заданий
1. В квадратной матрице [Aij], i,j=  заменить нулями элементы с четной суммой индексов, не превышающие некоторого числа X.
заменить нулями элементы с четной суммой индексов, не превышающие некоторого числа X.
2. Получить матрицу [Bij], i,j=  из матрицы [Aij], i,j=1 путем перестановки столбцов - первого с последним, второго с предпоследним и т.д.
из матрицы [Aij], i,j=1 путем перестановки столбцов - первого с последним, второго с предпоследним и т.д.
3,4. Получить новую матрицу [Вi,j], i,j=

из матрицы[Aij], путем перестановки сегментов в соответствии с рис. 4.1а и 4.1б
Рис. 4.1 а) Рис. 4.1 б)
5. В произвольной матрице [Aij] i=  ; j=
; j= 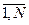
 найти минимальный и максимальный элементы, указать номера строк и номера столбцов, на пересечении которых они находятся.
найти минимальный и максимальный элементы, указать номера строк и номера столбцов, на пересечении которых они находятся.
6,7. Из одномерного массива [Xi] i= 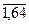 получить действительную квадратную матрицу 8*8, элементами которой являются числа x1,…,x64 расположенные в ней по схеме, приведенной на рис. 4.2а и 4.2б.
получить действительную квадратную матрицу 8*8, элементами которой являются числа x1,…,x64 расположенные в ней по схеме, приведенной на рис. 4.2а и 4.2б.
Рис. 4.2 а) Рис. 4.2 б)
8. В произвольной матрице [Aij] i=  ; j=
; j= 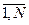
 столбец, содержащий максимальный элемент, заменить на сумму всех элементов матрицы.
столбец, содержащий максимальный элемент, заменить на сумму всех элементов матрицы.
9,10,11,12. Получить квадратную матрицу [Aij], i,j=

следующего вида:
13. Получить матрицу [Cij] i,j=  из матриц [Aij] i,j=
из матриц [Aij] i,j=  и [Bij] i,j=
и [Bij] i,j=  путем умножения элементов каждой строки матрицы [Aij] на максимальный элемент соответствующей строки матрицы [Bij].
путем умножения элементов каждой строки матрицы [Aij] на максимальный элемент соответствующей строки матрицы [Bij].
14. В квадратной матрице [Aij] i,j=  среди элементов расположенных ниже главной диагонали найти минимальный, а среди элементов выше главной диагонали – максимальный. Вывести координаты этих элементов.
среди элементов расположенных ниже главной диагонали найти минимальный, а среди элементов выше главной диагонали – максимальный. Вывести координаты этих элементов.
15. В квадратной матрице [Aij] i,j=  среди элементов, расположенных ниже побочной диагонали, определить количество положительных элементов, а среди элементов выше побочной диагонали – количество отрицательных элементов.
среди элементов, расположенных ниже побочной диагонали, определить количество положительных элементов, а среди элементов выше побочной диагонали – количество отрицательных элементов.
16. Из квадратной матрицы [Aij] i,j=  сформировать одномерный массив [Xi] i=
сформировать одномерный массив [Xi] i= 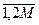 по следующему правилу: элементами одномерного массива [Xi] с нечетными индексами будут элементы главной диагонали [Aij], с четными – побочной диагонали [Aij].
по следующему правилу: элементами одномерного массива [Xi] с нечетными индексами будут элементы главной диагонали [Aij], с четными – побочной диагонали [Aij].
17. Сформировать одномерный массив [Xi] i=  из сумм положительных элементов строк матрицы [Aij] j,i=
из сумм положительных элементов строк матрицы [Aij] j,i=  , попутно определяя номера строк матрицы [Aij] i,j=
, попутно определяя номера строк матрицы [Aij] i,j=  , в которых отсутствуют положительные элементы.
, в которых отсутствуют положительные элементы.
18. Сформировать одномерный массив [Bi] i=  из минимальных элементов строк прямоугольной матрицы[Aij] i=
из минимальных элементов строк прямоугольной матрицы[Aij] i=  , j=
, j= 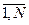 . Подсчитать количество элементов массива [Bi] попавших в интервал (x,y).
. Подсчитать количество элементов массива [Bi] попавших в интервал (x,y).
19. Сформировать одномерный массив [Bi] i=  из максимальных элементов столбцов прямоугольной матрицы [Aij] i=
из максимальных элементов столбцов прямоугольной матрицы [Aij] i=  , j=
, j= 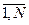 В массиве [Bi] поменять местами первый отрицательный и последний положительный элементы.
В массиве [Bi] поменять местами первый отрицательный и последний положительный элементы.
20. В квадратной матрице [Aij] i,j=  заменить элементы главной и побочной диагоналей на минимальный элемент главной диагонали.
заменить элементы главной и побочной диагоналей на минимальный элемент главной диагонали.
21. В произвольной матрице [Aij] i=  , j=
, j= 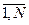 поменять местами строку, содержащую минимальный элемент, со строкой, содержащей максимальный элемент.
поменять местами строку, содержащую минимальный элемент, со строкой, содержащей максимальный элемент.
22. В квадратной матрице [Aij] i,j=  , найти максимальный элемент среди элементов, стоящих на главной и побочной диагоналях, и поменять его местами с элементом, стоящим на пересечении этих диагоналей.
, найти максимальный элемент среди элементов, стоящих на главной и побочной диагоналях, и поменять его местами с элементом, стоящим на пересечении этих диагоналей.
23. В квадратной матрице [Aij] i,j=  определить номер столбца матрицы, имеющего наибольшую сумму элементов. Поменять этот столбец со строкой имеющей наименьшую сумму элементов.
определить номер столбца матрицы, имеющего наибольшую сумму элементов. Поменять этот столбец со строкой имеющей наименьшую сумму элементов.
24,25
. В квадратной матрице [Aij] i,j=

найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы рис. 4.3а и 4.3б.
Рис. 4.3. а) Рис. 4.3.б)
 из матрицы[Aij], путем перестановки сегментов в соответствии с рис. 4.1а и 4.1б
из матрицы[Aij], путем перестановки сегментов в соответствии с рис. 4.1а и 4.1б
 следующего вида:
следующего вида:
 найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы рис. 4.3а и 4.3б.
найти наибольшее из значений элементов, расположенных в заштрихованной части матрицы рис. 4.3а и 4.3б.



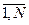
 найти минимальный и максимальный элементы, указать номера строк и номера столбцов, на пересечении которых они находятся.
найти минимальный и максимальный элементы, указать номера строк и номера столбцов, на пересечении которых они находятся.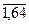 получить действительную квадратную матрицу 8*8, элементами которой являются числа x1,…,x64 расположенные в ней по схеме, приведенной на рис. 4.2а и 4.2б.
получить действительную квадратную матрицу 8*8, элементами которой являются числа x1,…,x64 расположенные в ней по схеме, приведенной на рис. 4.2а и 4.2б.




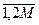 по следующему правилу: элементами одномерного массива [Xi] с нечетными индексами будут элементы главной диагонали [Aij], с четными – побочной диагонали [Aij].
по следующему правилу: элементами одномерного массива [Xi] с нечетными индексами будут элементы главной диагонали [Aij], с четными – побочной диагонали [Aij].




