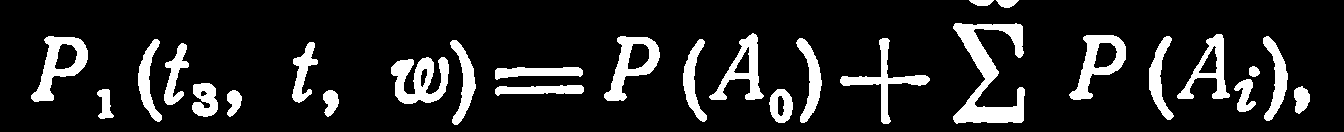О методах анализа надежности систем с временной избыточностью

Для анализа надежности систем с временной избыточностью используются две основные группы методов: аналитические и статистического моделирования. Аналитические методы более удобны при изучении общих свойств резервирования, поскольку они позволяют проанализировать характеристики надежности в большом диапазоне параметров и в любых интервалах времени. Они дают возможность проследить тенденции к изменению основных характеристик надежности и выяснить структуру процесса функционирования системы. Методы статистического моделирования позволяют анализировать сложные модели надежности, хотя и не обладают большой общностью.

При аналитическом исследовании процесс функционирования технической системы формализуется и сводится обычно к модели полумарковского или многомерного марковского процесса. Приведем здесь краткую характеристику четырех основных методов, которые мы будем использовать в дальнейшем. Два из них (метод перебора гипотез и метод условных вероятностей) опираются на прямое вычисление вероятностей, а два других (дифференциальный и интегральный) требуют составления и последующего решения уравнений относительно вероятности безотказного функционирования системы с временной избыточностью.

Метод перебора гипотез основан на использовании формулы полной вероятности.

i=1,

где, Я(Ло)—вероятность того, что до выполнения задания не произойдет ни одного нарушения работоспособности системы; P(Ai) — вероятность того, что до выполнения задания произойдет ровно г нарушений работоспособности. Все слагаемые начиная со второго, составляют приращение вероятности из-за введения временной избыточности. При достаточно редких нарушениях работоспособности ряд хорошо сходится и для получения удовлетворительной точности достаточно вычислить несколько первых его членов. Нахождение выражений для Р(А{) сводится к многократному интегрированию известных функций.

При выводе формулы по существу, используется метод асимптотического разложения вероятностей состояний сложных систем по степеням малого параметра. Основная трудность применения этого метода состоит в необходимости оценить остаточный член. Ее удается избежать, вычисляя двустороннюю оценку точного решения. Для этого в дополнение к составим еще одно выражение для вероятности срыва функционирования в виде положительного ряда,

где Р{Вх)—вероятность того, что срыв функционирования возникает до момента t, причем до него происходит ровно i нарушений работоспособности.

Вычисляя несколько первых членов ряда, из и находим оценку снизу для Pi (4 t, w) и Qi(4, t, w) соответственно. Затем по формуле оценим вероятность безотказного функционирования сверху.

Двусторонние оценки оказываются полезными и для контроля правильности вычислений.

Метод условных вероятностей основан на представлении случайного времени выполнения задания в виде некоторой функции случайных величин: наработки системы, времени восстановления, количества нарушений работоспособности и т. д. Вероятность безотказного функционирования находится сначала при условии, что все случайные величины, кроме одной, принимают фиксированные значения. Затем условия постепенно снимаются с учетом заданных распределений случайных величин и находится искомое выражение, записываемое обычно в операционной форме.

Дифференциальный метод получил свое название потому, что система уравнений для вероятности безотказного функционирования является в этом случае системой дифференциальных уравнений. При их составлении задаются приращения поочередно всем аргументам искомых функций и находится связь последних со значениями этих же функций в точке (4, t, w). Устремляя затем приращения аргументов к нулю, получают систему дифференциальных уравнений в частных производных с начальными и граничными условиями, отражающими поведение случайного процесса функционирования при 4=0,^=0 и w = где Wk — некоторые предельные значения векторного аргумента w. При использовании интегрального метода вводятся вероятности безотказного функционирования P(i)(4, 4, w) при условии,, что в начале оперативного интервала времени изучаемая техническая система находится в состоянии i. Рассматривая участок траектории процесса функционирования до первого изменения состояния, устанавливают между этими вероятностями связь в виде следующего интегрального соотношения: где PW(t3,w)—вероятность безотказного функционирования при условиях, что ^и = 0 и что за время от начала оперативного интервала до момента выполнения задания система ни разу не выйдет из состояния i. Интегральный оператор Lik здесь является вольтерровским оператором с разностным ядром. Выяснение его вида входит в задачу анализа конкретной системы и об этом будет идти речь далее. Систему уравнений 14 назовем системой интегральных уравнений в нормальной форме. В некоторых случаях ее удается свести к одному интегральному уравнению Вольтерра второго рода с разностным ядром:

P(t3, /и, w)=P(i3, w)+LP(t3, ta, w),

где L — интегральный оператор, порядок которого равен порядку системы уравнений Уравнении назовем каноническим уравнением для вероятности безотказного функционирования системы с временной избыточностью.

Составленные уравнения еще не являются гарантией того, что удастся получить приемлемые для ручного счета точные и даже приближенные формулы. Поэтому в некоторых случаях целесообразно находить показатели надежности численным решением уравнений на ЦВМ.