ЭНЕРГЕТИЧЕСКИЙ МЕТОД РАСЧЕТА ПЫЛЕУЛОВИТЕЛЕЙ
При выборе оптимального варианта очистной установки в каждом конкретном случае необходимо провести сравнительную оценку ожидаемых степеней очистки. Значительное число различных механизмов осаждения, способствующих улавливанию взвешенных частиц, а также разнообразие форм гидродинамического взаимодействия газов и жидкости в мокрых пылеуловителях пока не позволяет разработать точный аналитический метод расчета их эффективности. Поэтому на практике нашли применение несколько приближенных методов расчета. Эффективность очистки газов от пыли и выбор аппарата в значительной степени зависят от свойств улавливаемой пыли, из которых основными являются дисперсность, плотность (истинная, насыпная, кажущаяся), склонность к слипанию, сыпучесть, абразивность, смачиваемость, гигроскопичность и растворимость. Гигроскопичность и растворимость частиц способствуют их улавливанию в аппаратах мокрого типа. Применение многих пылеулавливающих аппаратов ограничено слипаемостью улавливаемой пыли. Абразивность улавливаемой пыли учитывается при выборе скорости запыленных газов, толщины стенок аппаратов. Основным параметром при выборе пылеуловителя является размер частиц. Дисперсный состав пыли можно представить в виде содержания (по числу или по массе) частиц различных фракций. Фракцией называют относительную долю частиц, размеры которых находятся в определенном интервале значений, принятых в качестве нижнего и верхнего пределов. Дисперсный состав чаще всего задается в виде таблиц экспериментальных данных. Наиболее удобным является графическое изображение дисперсного состава пыли в виде интегральных кривых. Для аналитического описания кривых распределения частиц по массе предложены различные формулы. Большинство промышленных пылей подчиняется нормально-логарифмическому закону распределения частиц по размерам. В этом случае интегральная кривая распределения частиц по размерам на логарифмически вероятностной координатной сетке изобразится прямой линией и может быть выражена аналитически в виде
где x = (lgd – lgdm)/lgσ; (3.2) где D(d) — функция распределения по проходу частиц; dm — медианный диаметр, при котором масса всех частиц анализируемой пыли меньше или крупнее dm составляет 50 %; lgσ — стандартное отклонение величины lg d.
Интеграл Ф(x) табулирован, поэтому его величину, соответствующую значениям х, находят по таблицам. Величину дисперсии σ c достаточной точностью можно определять по формуле σ = d84/dm = dm/d16, (3.3) где d16, d84 — диаметры частиц с содержанием фракций меньше 16 и 84 % соответственно.
Приближенно общую степень очистки можно определить, как сумму произведений парциальных степеней очистки (в %) на соответствующие доли массы фракций Δφi/100
Если Δφi малая величина, то точное значение общей степени очистки выразится в виде интеграла
Для расчета по формуле (3.4) могут быть использованы также кривые фракционных эффективностей (степеней очистки), полученные экспериментальным путем. Однако число таких зависимостей, приведенных в литературе, весьма невелико. Более того, они могут быть применены при расчетах эффективности очистки газов от пыли, характеризуемой параметрами, близкими к параметрам стандартной пыли, которая была использована при построении кривой фракционной эффективности, а также при условии идентичности гидродинамических режимов работы прогнозируемого и экспериментальных аппаратов.
Рис. 3.1. Номограмма для расчета эффективности пылеуловителей η с использованием интеграла вероятности (цифры на кривых – постоянные значения η: сплошные линии – для одного аппарата; пунктирные линии – для второго последовательно установленного аппарата)
Исследованиями показано, что для пылей, дисперсный состав которых подчиняется логарифмическому закону распределения, функции фракционных степеней очистки также подчиняются логарифмически нормальному закону распределения. Исходя из этого, общая степень очистки может быть выражена следующей зависимостью:
где x = (lgdm – lgd50)/ σч, ση — среднее квадратичное отклонение, соответственно по размерам частиц и фракционных коэффициентов очистки пылеуловителя.
Если известны величины dm, σ и параметры функции фракционной степени очистки d50, ση, то, вычислив по формуле (3.7) величину X, по таблице через Ф(х) находят значение общей степени очистки. Вместо вычислений по формуле (3.6) можно воспользоваться номограммами, построенными с использованием интеграла вероятности (рис. 3.1), на которых линии соответствуют постоянным η для различных значений lgσч/lgσ и lg(d50/dm)/lgσч. Основываясь на приведенных выше закономерностях, были предложены графические методы определения общей степени очистки по заданным значениям параметров dm, σ, dη, ση. Графический метод расчета разработан для скрубберов ВТИ, труб Вентури и ряда других пылеуловителей. Зависимость (3.7) можно использовать для определения функции фракционной степени очистки в инерционных пылеуловителях без оценки дисперсного состава улавливаемой пыли. Для этого достаточно испытать пылеуловитель на двух пылях различного дисперсного состава, определить соответствующие значения общей степени очистки и составить систему из двух уравнений. Как известно, функция фракционной степени очистки в аппарате при одном и том же режиме не зависит от дисперсного состава пыли и остается постоянной. Поэтому в полученной системе уравнений неизвестными остаются только две величины dη и ση. Величины η1, η2 известны из опыта; dml, σ1, dm2, σ2 известны из анализа дисперсного состава исходных пылей. Решая полученную систему уравнений, можно найти dη и ση. Существенным недостатком такого метода определения является необходимость проведения испытаний на двух видах различной пыли, что исключает возможность практического его применения в промышленных условиях, когда пылеуловитель работает на пылях примерно одного и того же состава. Исследованиями установлено, что кривая фракционной эффективности (КФЭ) для однотипных пылеуловителей характеризуется одним и тем же значением среднеквадратичного отклонения одного из двух параметров, характеризующих КФЭ. Например, для труб Вентури ση = 3,6. Существует также энергетический метод расчета мокрых пылеуловителей, например, скрубберов Вентури, основанный на зависимости степени очистки от затрат энергии на проведение очистки. Зависимость между эффективностью очистки газов и энергозатратами выражается формулой:
где Кч — удельная энергия соприкосновения, кДж на 1000 м3 газов; В и χ— константы, определяемые дисперсным составом пыли. Экспериментально установленные зависимости мощности контактирования от расхода воздуха, удельного расхода воды, гидравлического сопротивления и типоразмера мокрого пылеуловителя, как правило, можно представить в виде номограмм. Пользуясь этими номограммами, а также кривыми фракционной эффективности, ведут расчет степени очистки воздуха от пыли в данном мокром пылеуловителе. В результате обобщения теоретических и экспериментальных данных по эффективности различных конструкций мокрых пылеуловителей, разработан вероятностно-энергетический метод расчета, основанный на следующей зависимости:
Выражение (3.9) соответствует стандартным условиям: плотность пыли ρч = 1000 кг/м3 и вязкости газов μг = 18·10-6 Па·с. Зависимость (3.9) справедлива при условии, что дисперсный состав пыли на входе в аппарат подчиняется нормально-логарифмическому закону распределения частиц по размерам. При этом возможно решение двух противоположных задач: определение типа скруббера, обеспечивающего достижение необходимой степени очистки газов, и расчет эффективности пылеулавливания конкретного мокрого пылеуловителя, работающего в определенном гидродинамическом режиме.
Рассмотрим последовательность расчета при решении каждой задачи. Выбор типа скруббера, обеспечивающего необходимую степень очистки. Заданы: дисперсный состав пыли (dm и lgσч), плотность пыли ρч и вязкость газов μг при реальных условиях, а также требуемая эффективность пылеулавливания η.
Таблица 3.1 Значения lgση и Кч для скрубберов различного типа
где m — удельное орошение, мэ/м3; pж — давление распыливаемой жидкости, Па; ΔPp — гидравлическое сопротивление в зоне контакта (рабочей зоне) скруббера, Па.
1. Принимаем η = Ф(х) — нормальная функция распределения, значения которой табулированы. Затем рассчитываем реальную величину d*50, которую должен обеспечить прогнозируемый скруббер:
2. Приводим значение d50 к стандартным условиям
3. По формуле (3.8) рассчитываем величину Кч и необходимые для ее достижения гидродинамические параметры аппарата. После чего переходим к выбору типа скруббера.
|

 (3.1)
(3.1) (3.4)
(3.4) (3.5)
(3.5)
 (3.6)
(3.6) , (3.7)
, (3.7) , (3.8)
, (3.8) . (3.9)
. (3.9)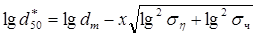 . (3.10)
. (3.10) . (3.11)
. (3.11)


