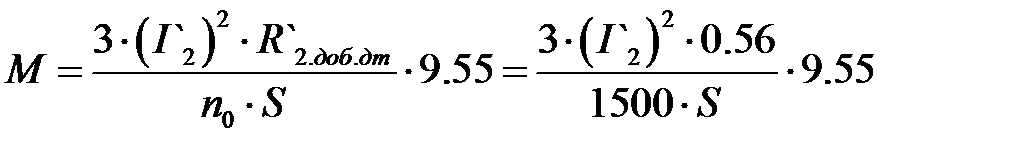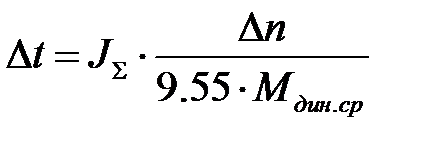Расчет статических и динамических характеристик для разомкнутой системы регулируемого электропривода
2.1. Расчет естественных характеристик ω=f(I), ω=f(М) регулируемого электропривода. Расчёт естественной механической характеристики произведем по следующему выражению:
Подставляя значения скольжения, получим соответствующие значения момента, развиваемого двигателем. Результаты расчета приведены в таблице 5. Таблица 5. Расчет естественной механической характеристики
По данным таблицы 5 построена естественная механическая характеристика двигателя, (рисунок 4). Рисунок 4 – Естественная механическая характеристика Для построения естественных электромеханических характеристик необходимо знать номинальный приведенный ток ротора и ток холостого хода, которые определяются по следующим выражениям: Номинальный приведенный ток ротора:
Номинальный ток холостого хода:
Тогда естественные электромеханические характеристики будут описываться следующими выражениями:
Расчет естественных электромеханических характеристик приведен в таблице 6. Таблица 6. Расчет естественных электромеханических характеристик
По данным таблицы 6 построены естественные электромеханические характеристики двигателя, (рисунок 5). Рисунок 5 – Естественные электромеханические характеристики двигателя
2.2. Расчет искусственных (регулировочных) характеристик ω=f(I), ω=f(М) регулируемого электропривода для заданного диапазона регулирования скорости Расчет искусственных механических характеристик осуществляется по следующим выражениям: Коэффициент, учитывающий добавочные сопротивления в роторной цепи:
Скорость холостого хода будет снижаться при изменении угла управления тиристоров инвертора:
Задаваясь несколькими углами управления находим коэффициент А по выражению:
Искусственная механическая характеристика будет описываться уравнением:
Расчет искусственных механических характеристик приведён в таблице 7. Таблица 7. Расчет искусственной механической характеристики
По результатам таблицы 7 построены искусственные механические характеристики системы, (рисунок 6). Рисунок 6 – искусственные механические характеристики Искусственные электромеханические характеристики системы рассчитаем из схемы замещения роторной цепи асинхронного вентильного каскада. Рисунок 7 – схема замещения роторной цепи асинхронного вентильного каскада. На данной схеме: Номинальное выпрямленное напряжение ротора:
Номинальное выпрямленное напряжение инвертора:
Эквивалентное индуктивное сопротивление двигателя, приведенное к ротору:
Эквивалентное активное сопротивление двигателя, приведенное к ротору:
Тогда искусственные электромеханические характеристики будут описываться уравнениями:
По данным выражениям произведён расчет искусственных электромеханических характеристик, который сведён в таблицу 8. Таблица 8. Расчёт искусственных электромеханических характеристик
По данным таблицы 8 построены искусственные электромеханические характеристики, (рисунок 8 и 9). Рисунок 8 – искусственная электромеханическая характеристика I2(s) Рисунок 9 – искусственная электромеханическая характеристика I1(s) 2.3. Расчет механических переходных характеристик ω=f(t) и М = f(t) при пуске, набросе и сбросе нагрузки при мгновенном изменении задания. Для построения переходных характеристик необходимо рассчитать добавочное пусковое сопротивление ротора, а также ток статора в режиме динамического торможения. Определяем величину добавочного сопротивления для работы на первой ступени регулирования.
Так как значение
В результате решения квадратного уравнения получаем два корня
Принимаем Определяем добавочное сопротивление для 1 ступени
Тогда механическая пусковая характеристика будет описываться уравнением:
Подставляя значения скольжения, получим соответствующие значения момента, развиваемого двигателем. Результаты расчета приведены в таблице 9. Таблица 9. Расчет пусковой механической характеристики
Точный расчет характеристики динамического торможения. Универсальная кривая намагничивания для асинхронных двигателей с фазным ротором типа МТ задается следующим образом: Таблица 10. Универсальная кривая намагничивания
Определяем эквивалентный ток статора. Постоянный ток при динамическом торможении Определяем величину сопротивления намагничивания для различных значений тока намагничивания. ПротивоЭДС в обмотке статора находим как Тогда Таблица 11. Значения
Величина
Определяем значение скольжения S, соответствующие значению тока намагничивания по выражению:
Значения S, полученные при отрицательном значении подкоренного выражения, отбрасываются и в дальнейших расчетах не участвуют. Найденные значения заносим в таблицу 12. Таблица 12. Значения скольжения, для различных
Определяем приведенный ток ротора соответствующий найденным значениям скольжения: Полученные значения заносим в таблицу 13. Таблица 13. Значения тока
Рассчитываем механическую характеристику двигателя в режиме динамического торможения для соответствующих значений S:
Полученные значения заносим в таблицу 14. Таблица 14. Значения момента М для значений S
Ориентировочно момент инерции механизма можно определить как:
Суммарный момент инерции привода:
Время переходного процесса: Таблица 15. Пуск
Таблица 16. Резкое изменение угла управления с β=830 на β=620
Таблица 17. Динамическое торможение
По данным таблиц 15 – 17 строим графики переходных процессов, (рисунок 10).
Рисунок 10 – Механические переходные характеристики
|

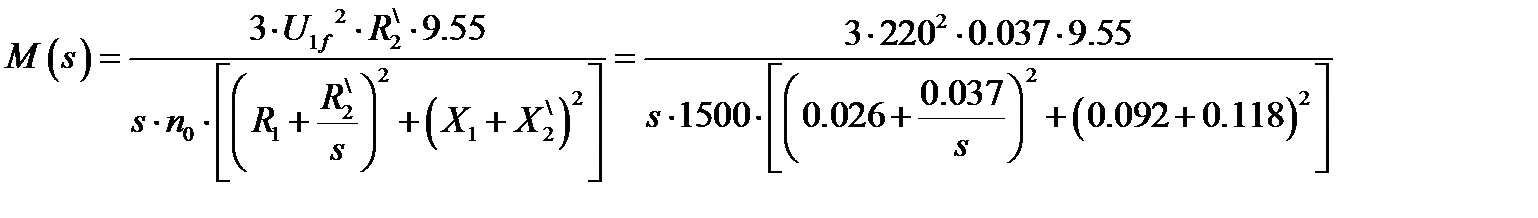

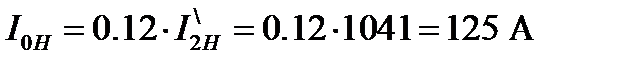
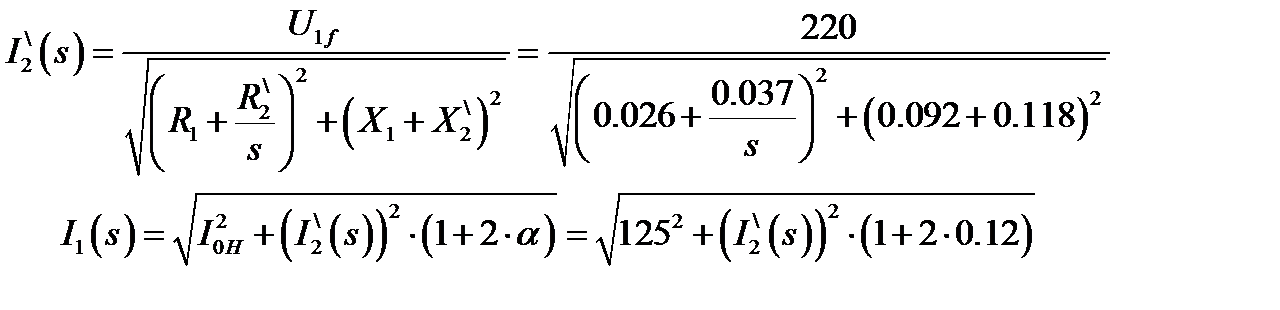



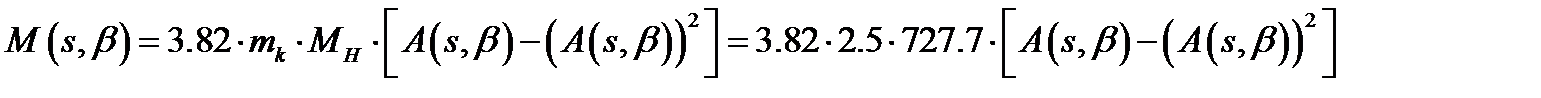

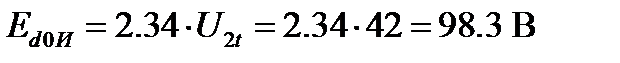

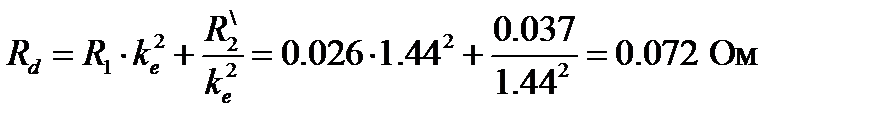
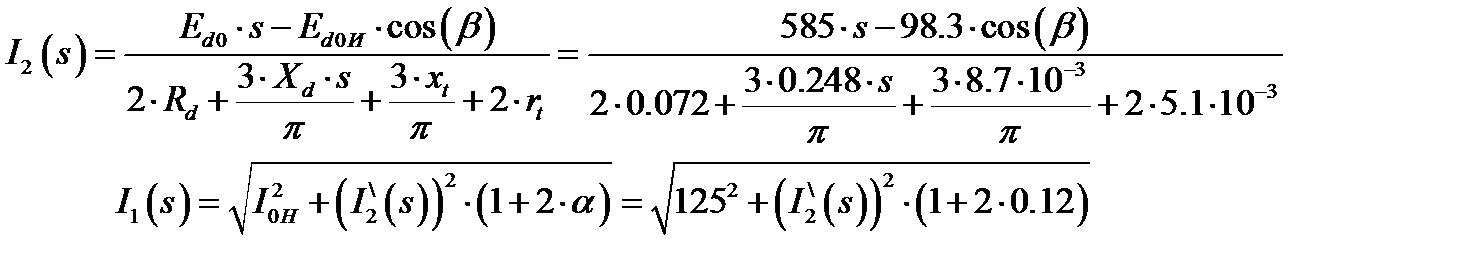

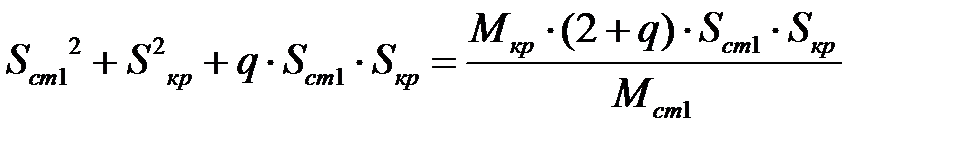
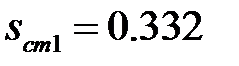 получаем:
получаем: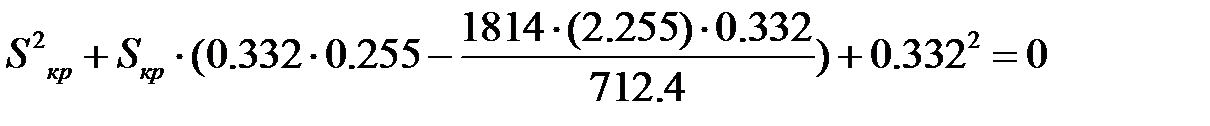
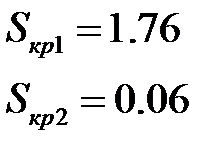

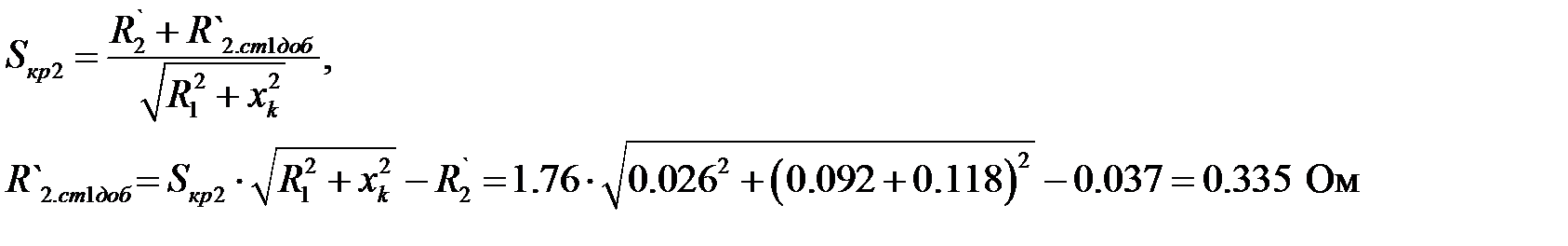





 , тогда эквивалентный ток
, тогда эквивалентный ток  .
.
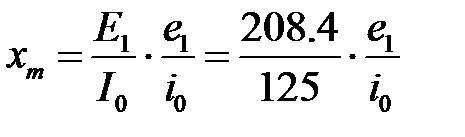 . Полученные значения сведем в таблицу 11.
. Полученные значения сведем в таблицу 11. для различных
для различных 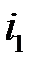 .
.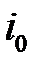

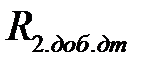 определяется из выражения
определяется из выражения
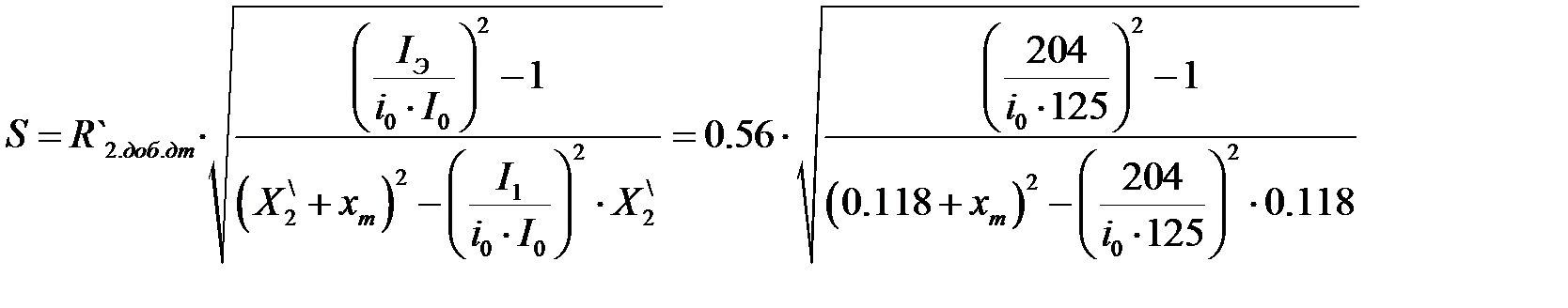
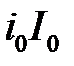 .
.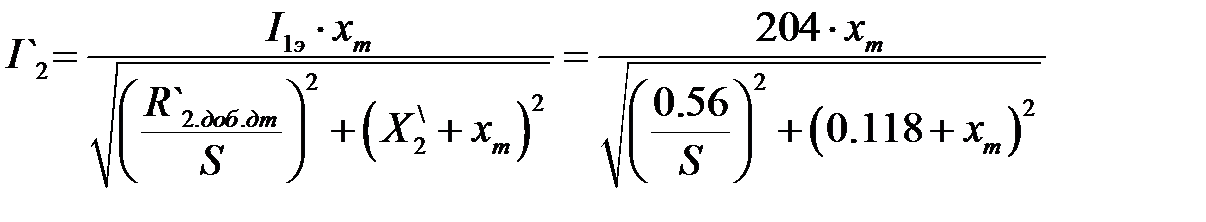
 , для различныхS.
, для различныхS.