П1 Ортогональные разложения функций
Широко известно использование аппарата Фурье для гармонического анализа детерминированных сигналов, при котором исходная функция разлагается в ряд по элементарным тригонометрическим функциям. Однако аппарат Фурье не является е Можно заданную в интервале времени 0-Т функцию ¦(t) разлагать в ряд по любым другим функциям jk(t), принятым в качестве элементарных:
Сходимость этого ряда всегда обеспечивается. Задача разложения всегда сводится к выбору функций jk(t) и определению коэффициентов разложения Ck. Коэффициенты Ck наиболее легко определяются, если функции jk(t) обладают свойством ортогональности. Функции называют ортогональными, если для них выполняется условие:
Умножая левую и правую части уравнения (1) на jk(t) и интегрируя на интервале 0-Т, с учетом ортогональности получим
Второе условие, которым необходимо руководствоваться при выборе функций разложения, заключается в упрощении анализа при теоретических исследованиях. Для точного воспроизведения функции при динственным. представлении ее в виде ряда необходимо суммировать в общем случае бесконечное число членов. В некоторых случаях допустимо представление функций с некоторой погрешностью. При этом в разложении (1) можно ограничиться конечным числом членов:
Погрешность представления функции удобно оценивать величиной среднеквадратичной ошибки
При выборе функций разложения в этом случае необходимо руководствоваться условием обеспечения минимума ошибки при заданном числе членов ряда. При N®¥ величина среднеквадратичной ошибки стремится к нулю, так как
Последнее выражение аналогично равенству Парсеваля, используемому в аппарате Фурье. Таким образом, всякую функцию можно с некоторой погрешностью представить в виде ряда с конечным числом членов. Представление непрерывного колебания в виде набора конечного числа функций или чисел называют иногда дискретизацией. Возможность представления функции в виде конечного ряда позволяет осуществлять следующий способ передачи некоторого сигнала S(t). На передающем конце сигнала S(t) можно разложить в ряд по выбранным функциям jk(t) и передавать не сигнал, а лишь коэффициенты разложения Ck. На приемном конце, имея генераторы функций jk(t) по принятым коэффициентам можно восстановить переданный сигнал. Следовательно, с этой точки зрения в качестве функций разложения необходимо выбирать такие, которые легко генерировать. Ниже рассматриваются два вида ортогональных разложений: разложение Фурье по гармоническим функциям и разложение Котельникова по функциям отсчетов.
|

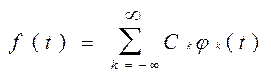 (1)
(1)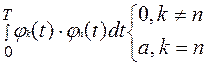 (2)
(2)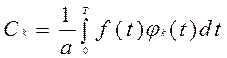 (3)
(3)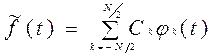 (4)
(4)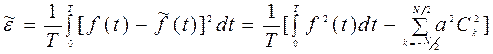 (5)
(5)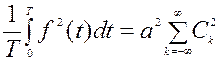 (6)
(6)


