П2 Дискретизация функций рядами Фурье
Рассмотренное выше в п.1.1 представление сигналов в виде ряда Фурье является типичным примером ортогонального разложения. Семейство тригонометрических функций 1, Cosw0t, Sinw0t, Cos2w0t, Sin2w0t,..., Cosnw0t, Sinnw0t,... является ортогональным на интервале 0¸T:
Обычно в ряд Фурье принято разлагать периодические функции, а для непериодических функций использовать интеграл Фурье. Однако в теоретических исследованиях используют представление в виде ряда Фурье и не периодических сигналов. Такой переход от интеграла к ряду Фурье приводит к тому, что непериодическая функция длительностью Т вне заданного интервала периодически продолжается с периодом Т. В технике связи широко используются синхронные системы связи. Синхронная работа предполагает, что в месте приема известны начало и длительность сигнала, и, следовательно, возможна установка «нулевых начальных условий» в момент окончания сигнала. В этих условиях устраняется влияние периодического продолжения непериодического сигнала, и указанная замена при анализе прохождения сигналов через системы связи не приводит к ошибкам. Таким образом, в указанных условиях любой сигнал можно охарактеризовать как непрерывным, так и дискретным спектром. Для реальных сигналов связи спектр является быстро убывающей функцией частоты. Поэтому часто бывает возможным ограничиться конечным числом членов в ряде Фурье.
при достаточной точности представления сигнала. Если приемлемая точность обеспечивается при числе гармоник, равном N/2, то полоса частот, необходимая для передачи такого сигнала (без постоянной составляющей), равна
Если на приемлемой стороне имеются управляемые генераторы гармонических составляющих, то для восстановления сигнала необходимо передать
чисел, определяющих коэффициенты разложения.
Заметим, что для некоторых сигналов представленных в виде конечного ряда может быть точным, например для сигналов, составленных из N/2 гармоник или отрезка одного гармонического колебания, если длительность сигнала кратна периоду основной гармоники. Величина В, равная удвоенному произведению длительности сигнала на ширину спектра частот, называется базой сигнала. Как известно из теории спектров, для наиболее часто встречающихся сигналов в виде отдельных импульсов произведение длительности на ширину спектра есть величина постоянная, имеющая порядок единицы D¦×Dt»1. Для таких сигналов, называемых простыми или узкополосными, база равна 2. В качестве сигналов можно использовать и такие, которые являются комбинациями простых сигналов (рис П2).
T0 t Т
рисунок П2
Эти комбинации представляют собой случайную последовательность простых сигналов. Такие сигналы называют составными или сложными. Для сложных сигналов ширина спектра будет такой же, что и для простых, а длительность и соответственно произведение 2¦bT будет больше. Сигналы, для которых база B=2¦bT>>1, называются широкополосными. П3 Теорема Котельникова. Любой сигнал с ограниченным спектром (бесконечный во времени) однозначно определяется своими отсчетами, взятыми через интервал времени
где U(k
Эта теорема утверждает, что если сигнал f(t) имеет преобразование Фурье Sf(w) отличное от нуля при частотах меньших 2pFm. То в отсчетах сигнала f(kDt) взятых через интервал Dt=1/2Fm содержится вся информация о непрерывной функции f(t). Из теоремы следует, что эти отсчеты содержат информацию о сигнале f(t) в любой момент времени. Однако частота отсчетов должна быть по крайней мере в два раза больше высшей частоты сигнала Fm.
|

 (7)
(7)
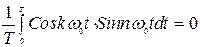 где w0=2p/Т
где w0=2p/Т (8)
(8) (9)
(9) (10)
(10) S(t)
S(t) S(t)
S(t)






 t
t т.е.
т.е.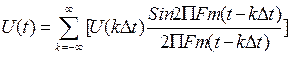 (11)
(11) t) - аналоговая величина
t) - аналоговая величина


