Приложение 5. Рисунок 5. Параллельное соединение звеньев
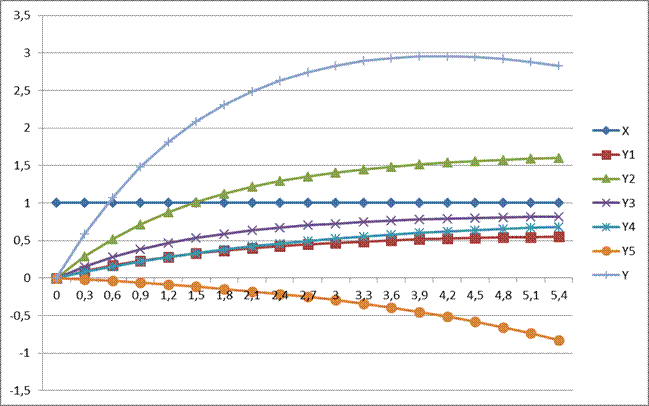
Рисунок 5. Параллельное соединение звеньев
Приложение 6
| t
| X
| Y1
| Y2
| Y3
| Y4
| Y5
| Y
| |
|
|
|
|
|
|
|
| | 0,3
|
| 0,089041
| 0,283812
| 0,152266
| 0,081282
| -0,01903
| 0,587367
| | 0,6
|
| 0,164412
| 0,5191
| 0,276931
| 0,154306
| -0,03988
| 1,074869
| | 0,9
|
| 0,228212
| 0,714161
| 0,378998
| 0,21991
| -0,06271
| 1,478573
| | 1,2
|
| 0,282218
| 0,875872
| 0,462564
| 0,278849
| -0,08771
| 1,811792
| | 1,5
|
| 0,327933
| 1,009935
| 0,530981
| 0,331799
| -0,11509
| 2,085557
| | 1,8
|
| 0,36663
| 1,121077
| 0,586997
| 0,37937
| -0,14508
| 2,308995
| | 2,1
|
| 0,399386
| 1,213217
| 0,632859
| 0,422107
| -0,17792
| 2,489649
| | 2,4
|
| 0,427114
| 1,289604
| 0,670407
| 0,460502
| -0,21389
| 2,63374
| | 2,7
|
| 0,450585
| 1,352931
| 0,701149
| 0,494996
| -0,25328
| 2,746385
| |
|
| 0,470452
| 1,405431
| 0,726318
| 0,525985
| -0,29641
| 2,831773
| | 3,3
|
| 0,48727
| 1,448955
| 0,746925
| 0,553826
| -0,34366
| 2,893319
| | 3,6
|
| 0,501506
| 1,485037
| 0,763797
| 0,578838
| -0,3954
| 2,933781
| | 3,9
|
| 0,513556
| 1,514951
| 0,77761
| 0,601308
| -0,45206
| 2,955366
| | 4,2
|
| 0,523756
| 1,53975
| 0,78892
| 0,621496
| -0,51412
| 2,959806
| | 4,5
|
| 0,532391
| 1,560309
| 0,798179
| 0,639632
| -0,58208
| 2,948434
| | 4,8
|
| 0,5397
| 1,577353
| 0,80576
| 0,655926
| -0,65651
| 2,922232
| | 5,1
|
| 0,545886
| 1,591484
| 0,811966
| 0,670564
| -0,73802
| 2,88188
| | 5,4
|
| 0,551124
| 1,603198
| 0,817048
| 0,683715
| -0,82729
| 2,827793
|
Таблица 3.Значения с параллельным соединением звеньев
Приложение 7
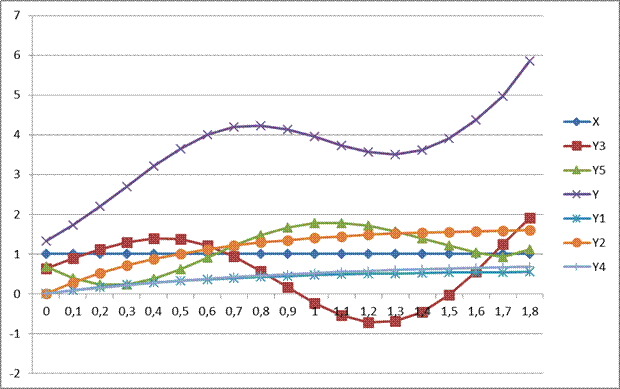
Рисунок 6. Параллельное соединение звеньев с заменойY3 и Y5 на колебательное звено
Приложение 8
| t
| X
| Y1
| Y2
| Y3
| Y4
| Y5
| Y
| |
|
|
|
| 0,639958
|
| 0,691671
| 1,33163
| | 0,1
|
| 0,089041
| 0,283812
| 0,888006
| 0,081282
| 0,386204
| 1,728344
| | 0,2
|
| 0,164412
| 0,5191
| 1,122468
| 0,154306
| 0,232864
| 2,193149
| | 0,3
|
| 0,228212
| 0,714161
| 1,303587
| 0,21991
| 0,235679
| 2,701549
| | 0,4
|
| 0,282218
| 0,875872
| 1,394949
| 0,278849
| 0,375897
| 3,207783
| | 0,5
|
| 0,327933
| 1,009935
| 1,369814
| 0,331799
| 0,617345
| 3,656826
| | 0,6
|
| 0,36663
| 1,121077
| 1,21674
| 0,37937
| 0,913643
| 3,99746
| | 0,7
|
| 0,399386
| 1,213217
| 0,943467
| 0,422107
| 1,216026
| 4,194203
| | 0,8
|
| 0,427114
| 1,289604
| 0,578218
| 0,460502
| 1,480589
| 4,236026
| | 0,9
|
| 0,450585
| 1,352931
| 0,167863
| 0,494996
| 1,673988
| 4,140362
| |
|
| 0,470452
| 1,405431
| -0,22719
| 0,525985
| 1,776963
| 3,95164
| | 1,1
|
| 0,48727
| 1,448955
| -0,54097
| 0,553826
| 1,78543
| 3,734514
| | 1,2
|
| 0,501506
| 1,485037
| -0,71186
| 0,578838
| 1,709285
| 3,562808
| | 1,3
|
| 0,513556
| 1,514951
| -0,69318
| 0,601308
| 1,569346
| 3,50598
| | 1,4
|
| 0,523756
| 1,53975
| -0,46272
| 0,621496
| 1,393097
| 3,615379
| | 1,5
|
| 0,532391
| 1,560309
| -0,02957
| 0,639632
| 1,209977
| 3,912735
| | 1,6
|
| 0,5397
| 1,577353
| 0,563139
| 0,655926
| 1,04695
| 4,383068
| | 1,7
|
| 0,545886
| 1,591484
| 1,240737
| 0,670564
| 0,924939
| 4,97361
| | 1,8
|
| 0,551124
| 1,603198
| 1,904854
| 0,683715
| 1,120083
| 5,862975
|
Таблица 4.Значения параллельного соединения звеньев с заменойY3 и Y5 на колебательное звено
Приложения 10
| № варианта
| k1
| T1
| k2
| T2
| k3
| T3
| k4
| T4
| k5
| T5
| |
|
|
|
|
|
|
|
|
|
|
| |
| 0,5
|
| 1,5
| 0,8
|
| 1,5
| 0,8
|
| 0,2
| -3,3
| |
| 0,51
| 1,1
| 1,52
| 0,9
| 0,98
| 1,5
| 0,8
| 2,1
| 0,2
| -3,3
| |
| 0,52
| 1,2
| 1,54
|
| 0,96
| 1,5
| 0,8
| 2,2
| 0,2
| -3,3
| |
| 0,53
| 1,3
| 1,56
| 1,1
| 0,94
| 1,5
| 0,8
| 2,3
| 0,2
| -3,3
| |
| 0,54
| 1,4
| 1,58
| 1,2
| 0,92
| 1,5
| 0,8
| 2,4
| 0,2
| -3,3
| |
| 0,55
| 1,5
| 1,6
| 1,3
| 0,9
| 1,5
| 0,8
| 2,5
| 0,2
| -3,3
| |
| 0,56
| 1,6
| 1,62
| 1,4
| 0,88
| 1,5
| 0,8
| 2,6
| 0,2
| -3,3
| |
| 0,57
| 1,7
| 1,64
| 1,5
| 0,86
| 1,5
| 0,8
| 2,7
| 0,2
| -3,3
| |
| 0,58
| 1,8
| 1,66
| 1,6
| 0,84
| 1,5
| 0,8
| 2,8
| 0,2
| -3,3
| |
| 0,59
| 1,9
| 1,68
| 1,7
| 0,82
| 1,5
| 0,8
| 2,9
| 0,2
| -3,3
| |
| 0,6
|
| 1,7
| 1,8
| 0,8
| 1,5
| 0,8
|
| 0,2
| -3,3
| |
| 0,61
| 2,1
| 1,72
| 1,9
| 0,78
| 1,5
| 0,8
| 3,1
| 0,2
| -3,3
| |
| 0,62
| 2,2
| 1,74
|
| 0,76
| 1,5
| 0,8
| 3,2
| 0,2
| -3,3
| |
| 0,63
| 2,3
| 1,76
| 2,1
| 0,74
| 1,5
| 0,8
| 3,3
| 0,2
| -3,3
| |
| 0,64
| 2,4
| 1,78
| 2,2
| 0,72
| 1,5
| 0,8
| 3,4
| 0,2
| -3,3
| |
| 0,65
| 2,5
| 1,8
| 2,3
| 0,7
| 1,5
| 0,8
| 3,5
| 0,2
| -3,3
| | | | | | | | | | | | | |
Таблица 6. Варианты значений параметров элементов системы

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
Методы прогнозирования национальной экономики, их особенности, классификация В настоящее время по оценке специалистов насчитывается свыше 150 различных методов прогнозирования, но на практике, в качестве основных используется около 20 методов...
Методы анализа финансово-хозяйственной деятельности предприятия
Содержанием анализа финансово-хозяйственной деятельности предприятия является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта хозяйствования с целью принятия оптимальных управленческих...
|
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
Примеры задач для самостоятельного решения. 1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P
1.Спрос и предложение на обеды в студенческой столовой описываются уравнениями: QD = 2400 – 100P; QS = 1000 + 250P...
Дизартрии у детей Выделение клинических форм дизартрии у детей является в большой степени условным, так как у них крайне редко бывают локальные поражения мозга, с которыми связаны четко определенные синдромы двигательных нарушений...
|
|






