Принцип построения алгоритма нечёткого вывода
Алгоритмизация и программная реализация моделей, построенных на методах нечёткой логики Нечёткая логика и теория нечётких множеств Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. Заде расширил понятие множества допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0 … 1], а не только 0 или 1. Такие множества были названы нечёткими. Так же автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества. Предметом нечёткой логики является построение моделей приближенных рассуждений человека и использование их в компьютерных системах. Принцип построения алгоритма нечёткого вывода Для того чтобы можно было применять простые правила, данные, передаваемые в блок регулирования на основе нечёткой логики, должны быть преобразованы. Преобразование заключается в следующем: Входные и выходные данные преобразовываются в лингвистические переменные. Каждая лингвистическая переменная характеризуется набором термов. Например, лингвистическая переменная температура может иметь следующие термы: «холодно», «норма», «жарко». Лингвистическая переменная уровень может иметь термы: «низкий», «нормальный», «высокий». Лингвистическая переменная регулирующий орган может иметь термы «открывать быстро», «открывать медленно», «не изменять», «закрывать медленно», «закрывать быстро». Каждый терм описывается своей функцией принадлежности Получив значение входной переменной Пример Допустим, имеется заслонка, открывающаяся по сигналу уровня, и правило: «Если уровень низкий, то заслонку открывать быстро». Имеется входная величина уровня Подобным образом происходит вычисление степени истинности для каждого правила. Этот процесс называется активизация (процедура логического вывода). Заключение из каждого правила собираются вместе для каждой лингвистической переменной. Этот процесс носит название аккумуляция (композиция). Например, после расчёта правил, мы получаем результаты для лингвистической переменной заслонка: «открывать быстро» - Зная степень истинности каждого терма выходной переменной, можно рассчитать её числовое значение. Эта процедура называется дефаззификацией (приведение к чёткости).
Таким образом, алгоритм работы нечёткой логики может быть разбит на следующие этапы: 1. Фаззификация входных переменных – функции принадлежности, определённые на входных переменных, применяются к их фактическим физическим значениям, затем происходит определение степени истинности каждой предпосылки каждого правила. 2. Активизация заключений правил нечёткой логики – значение истинности для предпосылок каждого правила применяется к заключениям каждого правила, в результате имеем нечёткие подмножества для каждой переменной вывода и для каждого правила. 3. Аккумуляция заключений для каждой лингвистической переменной – все нечёткие подмножества вывода для каждого правила объединяются вместе, чтобы сформировать одно нечёткое множество для каждой переменной вывода или компромиссную выходную функцию 4. Дефаззификация выходных переменных – результат нечёткого вывода преобразуется в чёткое число.
|

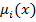 , которая может принимать значения от 0 до 1.
, которая может принимать значения от 0 до 1. , в блоке нечеткой логики вычисляется значение функции принадлежности каждого терма. Эта процедура называется фаззификацией (введение нечёткости). Результатом применения правила является величина, называемая степенью истинности (число от 0 до 1).
, в блоке нечеткой логики вычисляется значение функции принадлежности каждого терма. Эта процедура называется фаззификацией (введение нечёткости). Результатом применения правила является величина, называемая степенью истинности (число от 0 до 1).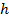 . Если уровень максимально высокий, то значение функции принадлежности
. Если уровень максимально высокий, то значение функции принадлежности 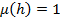 . Если уровень максимально низкий (либо в резервуаре отсутствует измеряемая среда), то
. Если уровень максимально низкий (либо в резервуаре отсутствует измеряемая среда), то 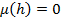 . В том случае, когда про уровень нельзя сказать, что он максимально высокий или максимально низкий, значение функции принадлежности будет дробным числом от 0 до 1, например, когда резервуар наполнен на половину,
. В том случае, когда про уровень нельзя сказать, что он максимально высокий или максимально низкий, значение функции принадлежности будет дробным числом от 0 до 1, например, когда резервуар наполнен на половину,  . Для различных степеней активации должны срабатывать разные правила, например, в первом случае заслонка не должна открываться, наоборот, если она открыта – её нужно закрыть максимально быстро. Во втором случае вступает в силу правило в примере – заслонка должна быть открыта максимально быстро. В третьем случае заслонка так же должна быть открыта, однако, т.к. уровень воды не низкий, то открывать быстро её не нужно – «заслонку открывать быстро, но на половину быстро». (вообще говоря, если в систему будет включено правило «Если уровень высокий, то заслонку закрывать быстро», то при наполовину пустом резервуаре может возникнуть терм «не изменять» и заслонка остановится).
. Для различных степеней активации должны срабатывать разные правила, например, в первом случае заслонка не должна открываться, наоборот, если она открыта – её нужно закрыть максимально быстро. Во втором случае вступает в силу правило в примере – заслонка должна быть открыта максимально быстро. В третьем случае заслонка так же должна быть открыта, однако, т.к. уровень воды не низкий, то открывать быстро её не нужно – «заслонку открывать быстро, но на половину быстро». (вообще говоря, если в систему будет включено правило «Если уровень высокий, то заслонку закрывать быстро», то при наполовину пустом резервуаре может возникнуть терм «не изменять» и заслонка остановится).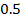 , «открывать медленно» -
, «открывать медленно» -  , «не изменять» -
, «не изменять» - 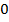 , «закрывать медленно» -
, «закрывать медленно» - 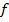 .
.


