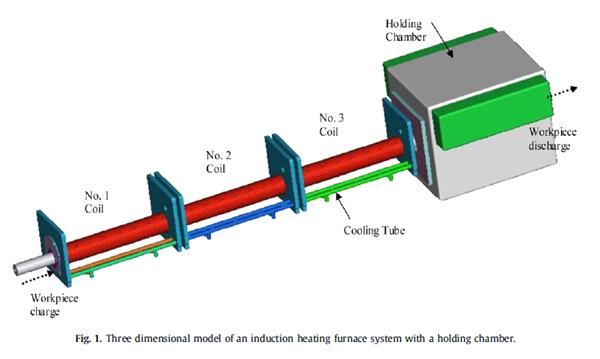
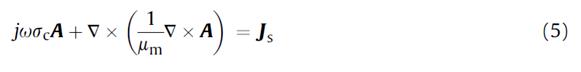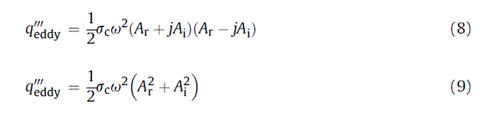Электромагнитное поле

(1)

Рассматриваемые электромагнитные явления подчиняются уравнениям Максвелла. Таким образом, электромагнитное поле вычисляется с использованием уравнений Максвелла, чтобы найти объем получаемой тепловой энергии в заготовке при индукционном нагреве.. Уравнение Максвелла можно упростить с помощью допущений квази-стационарного [18]:

 

где Н напряженность магнитного поля, J-плотность тока, В - напряженность магнитного поля, Е напряженность электрического поля, и угловая частота тока (i = 2pf, F = 60 Гц в данном исследовании) и J является комплексным числом, определяется 2 = -1. Гистерезисом и анизотропией пренебрегаем.
Представляем магнитный векторный потенциал А как

B = Vx A

 

предполагается, что ток в индукторе за время периода и тепловыделеня в заготовке производится вихревыми токами. Из приведенных выше уравнений, получаем основное уравнение:

где SC - электрическая проводимость материала, м-относительная магнитная проницаемость ферромагнитных материалов в зависимости от температуры Т, и Js - плотность тока, наведенного в индукторе [19].
Предполагается, что электромагнитное поле является осесимметричным так, что магнитный векторный потенциал А и плотность тока Js, которые являются постоянными и зависят от времени, а оно меняется. Эта задача была смоделирована с помощью осесимметричных допущений и геометрии, изображающей эти допущения, показана на рис. 2. Как показано на рис. 2, граничные условия, связанные с главным уравнением (5) заключаются в следующем:

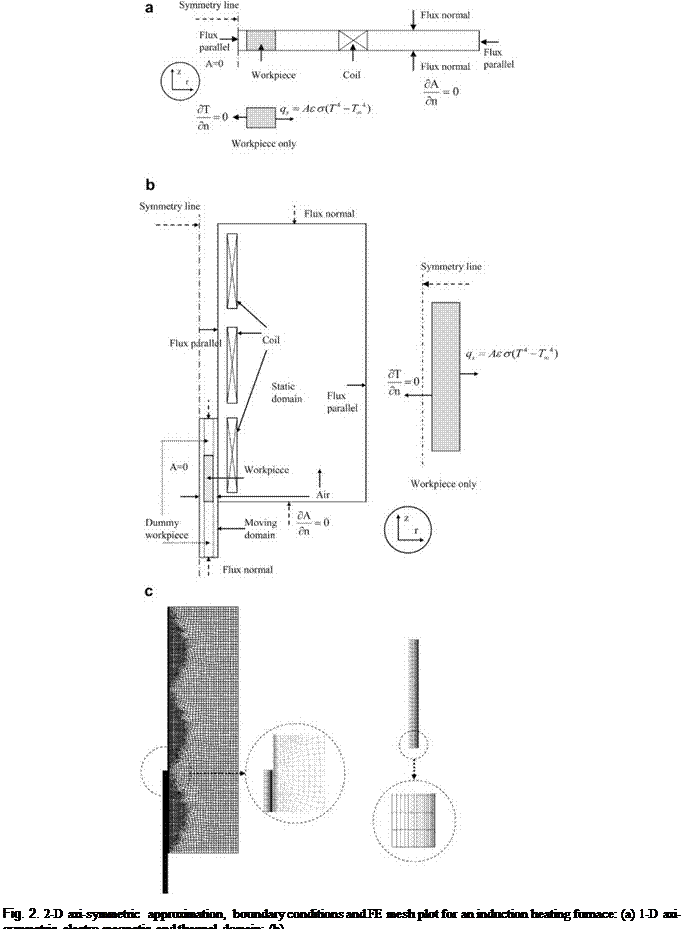
где n - единица нормали к границе. Границы расчетной области параллельны, и им параллелен магнитный поток (A = 0AT г = 0), поскольку направление индуцированного магнитного поля параллельно в продольном направлении заготовки. Кроме того, предполагается, что внешнее магнитное поле на катушке равно нулю, поэтому узлы на внешней кромке соединены (А = константа) так, что граничные условия взаимно накладываются. На других границах, перпендикулярных к оси симметрии, граничные условия являются естественными.

Решая это уравнение, мы можем получить объем выделяемой тепловой энергии (Вт/м3) вихревыми токами, вызванными в конкретный временной промежуток электромагнитным полем следующим образом:

 

где r - обозначает действительную часть, а i - обозначает мнимую комплексно-сопряженную часть.

2.2 Тепловое поле

 

Математическая модель, которая показывает тепловые явления связана с уравнением диффузии следующим образом:

 

 

где Т температура, т время, р плотность массы, Ср - теплоемкость, а к - это теплопроводность.
Для одномерного анализа, потери тепла при излучении с поверхности заготовки учитываются, однако, они не учитываются при двумерном анализе. Как показано на рис.2, тепловые граничные условия для одномерной внешней поверхности следующие:

 

jAi)

 

(9)

0, at r

r

(1 2)

9T

0, at

r

ro

(1 3)

9T

0, at r

r

 

где q_s (W) - излучаемая мощность от тела площадью А (м²) при температуре Т (К), коэффициент излучения (0.7 в этом исследовании), с постоянная Стефана-Больцмана (W/m²/K⁴), T_N - температура окружающей среды (К), r - внутренний радиус рассматриваемой заготовки, и р_о - внешний радиус рассматриваемой заготовки. Следует отметить, что условием конвекции на границе можно пренебречь, так как она равна 3% по сравнению с излучением, когда разница температуры между заготовкой и окружающей средой намного больше [20].