Двухмерный расчет

 

Второй пример - нагрев 2-D, имеющий адиабатические условия на внутренней поверхности заготовки, как 1-D случае. А остальные условия такие же, как и в первом примере (одномерный анализ). В отличие от одномерного анализа, конкретные действия с выбранными заготовками на начальном этапе показаны на рис. 2, делаем вывод: условные заготовки используются для того, чтобы неточностей магнитного поля вокруг выбранных заготовок. Цель состоит в том, чтобы получить наиболее точное распределение температуры, а это возможно только для конкретной заготовки внутри индукционного нагревательного устройства из-за конечного эффекта, как показано на рис. 2а.
Типовые контуры магнитного векторного потенциала показывающие динамический эффект движущейся заготовки с изменением времени показаны на рис. 6. Как показано на рис. 6, магнитный векторный потенциал в области дальнего поля, далеко от наружной поверхности заготовки, уменьшается независимо от изменения во времени после наведения ЭДС в заготовках. С другой стороны, контурные линии сконцентрированы вдоль наружной поверхности заготовки. Закрытые петли из линий постоянно меняются пока заготовки проходят время после загрузки в индукционную печь. Кроме того, как изображено на поверхности, мы знаем, что сила поля в пустом воздушном зазоре между заготовкой и индуктором не зависит от обрабатываемой детали, но вихревые токи в заготовке стремятся к полному потоку, согласно вихревой теории тока.

В результате, выпуклые профили магнитного потока появляются, когда превышается температура Кюри, происходит потеря магнитных свойств и увеличивается глубина проникновения (около 1,8 мм в этом вычислении) по аналогичной схеме, когда наступает время.
На Рис. 7 показаны изотермы внутри заготовки, за которыми мы следим в течении времени после загрузки заготовок в индукционную печь. На рис. 7а, линии распределения температуры почти параллельны вдоль направления длины заготовки сразу после загрузки заготовки (при Т = 30 с). Тем не менее, изотермические линии лежат вдоль заготовки, передаются в печи с непрерывной скоростью, аи разности температур становятся меньше во внутренней области заготовок, как показано на рис. 7b, в, г.
Рис. 8 показывает температурное изменение внутри заготовки относительно позиций (1) - (9) загрузки, как показано на схеме. Очевидно, что модель нагрева аналогична результату одномерного расчета (см. фиг. 5), но профиль температурных изменений в позиции (6), на пике круче, чем у 1-D случае. Мы считаем, что это может быть вызвано тем, что потоки, образующиеся внутри подвижной заготовки являются более сосредоточенными, чем с одномерном случае. По той же причине разница температур внутри заготовки выше, чем в одномерном случае.

 

 

 

 

 

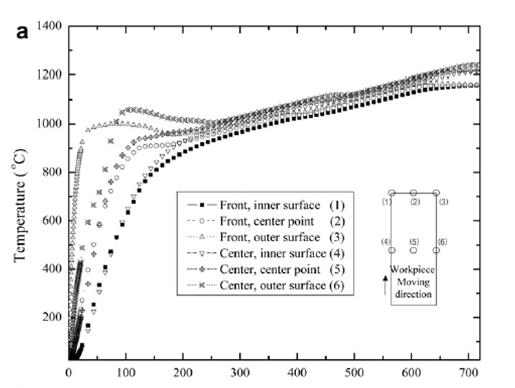
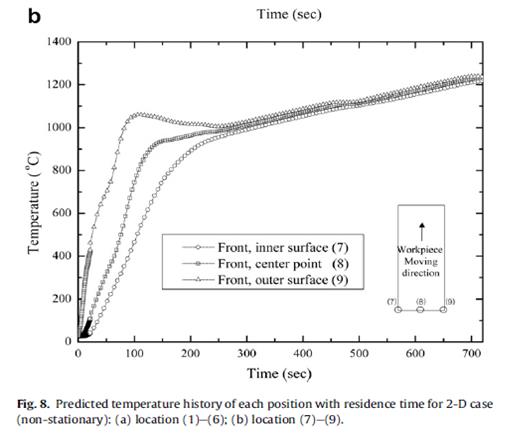
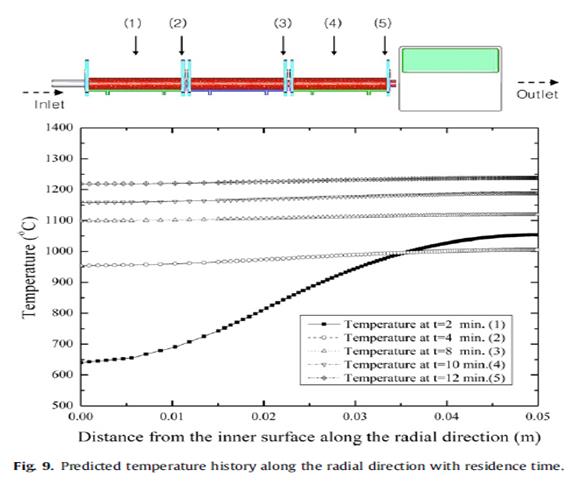
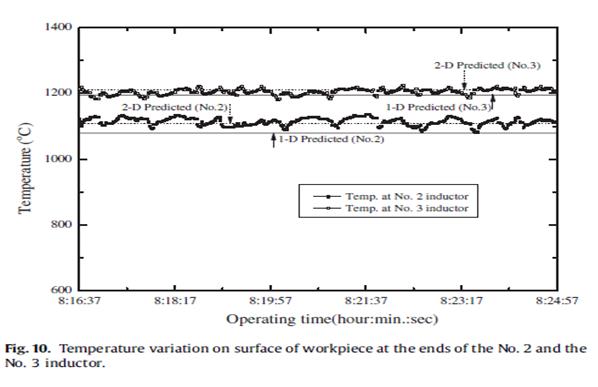
Наконец, на рис. 10 приведено сравнение между результатами измерений температуры поверхности, полученных с двух длин волн пирометра (Уильямсон Pro 220) и предполагаемых результатов, приведенных на рис. 5 и 8. Для двух измеренных данных, верхняя кривая представляет собой распределение температуры, измеряемой на концвх № 3, а нижняя часть представляет температуру распределения, измеряемую на концах № 2. Как показано на рис. 10, найденные расхождения, скорее всего, из-за неточности пирометров, идеализации геометрической реальности (осесимметричной геометрии), проблемы выравнивания детали внутри канала катушки, и так далее. Тем не менее, как правило, хорошее совпадение наблюдается в трех случаях (1-D анализа, 2-D анализа и экспериментальном результате), при том, что измеренные позиции фиксируются для сравнения температур.

Кроме того, время выдержки составляет около 65 с, если выбранные позиции привязанны к точкам (7), (8) и (9), так как они начинаются с Т = 0 с, как показано на рис. 8. Внимательное рассмотрение рис. 8 также показывает, что распределение температуры вдоль радиального направления заготовки становится почти равномерным от катушки № 2, как и при одномерном случае (см. рис. 5). Кроме того, разница температур внутри заготовки несколько выше, чем в одномерном случае, это может быть вызвано кривой магнитных полей из-за динамических эффектов, представленных в этом расчете, в отличие от 1 -D случае. Кроме того, интересно, в сравнении изменений температур 1 -D случае (см. рис. 5) и 2 -D случай вдоль позиций (7) через (9) (рис. 8, б), было установлено, что аналогичные модели были получены, как показано на рис. 5 и 8b.
Рис. 9 показывает градиент распределения температуры от внутренней поверхности заготовки, вдоль радиального направления (позиций (4) по (6) на рис. 8) в течение времени нахождения. Как показано на рис. 9, мы знаем, что есть некоторые явные различия температуры в радиальном направлении внутри заготовки до т = 2 мин (позиция (1)) после загрузки в печь, но они становятся почти равномерными после (т = 4 мин), то есть, когда заготовка не доходит до конца индуктора № 1.

Итоги

В этой статье мы представили осесимметричную динамическую модель, применимую к заготовкам, движущимся относительно индуктора. Преимущество этой модели в том, что она может повысить точность расчета потерь на вихревые токи и может быть применена для задач с переменным полем, где выбранные заготовки проходят через вихревое изменяющееся магнитное поле.

Вклад данной работы двойной. Во-первых, она предлагает связь электромагнитной и тепловой задач для численного анализа системы индукционного нагрева, подчеркивая динамический эффект заготовок, движущихся относительно индуктора. Во-вторых, она обеспечивает экспериментальную оценку представленной модели индукционного нагрева круглых заготовок.

Связанные электромагнитные и тепловые задачи, описывающие процесс индукционного нагрева, анализируются и обсуждаются.

Правильность нашего подхода подтверждается при сравнении полученных результатов с результатами, полученными от стационарного анализа 1 -D и измерений. По сравнению с результатами измерений, вычисляемые результаты представленной модели оказываются более точными, чем у обычного или стационарной модели.