Понятие определённого интеграла.
Определение. Пусть функция у=f(x)- определена и ограничена на промежутке [a, b] тогда суммы вида åf(zi)Dxi называются интегральными суммами функции f(x) на [a, b]. Определение. (Определённого интеграла). Предел интегральных сумм, если он существует и не зависит ни от способа разбиения промежутка [a, b] на элементарные части, ни от выбора точек zi, при условии, что l=maxçDxiç®0 называется определённым интегралом и обозначается
Замечание. Из первых двух задач следует физический и геометрический смысл определённого интеграла 1). b 2). òf(x)dx – S – площадь криволинейной трапеции, ограниченной a функцией f(x), x=a; x=b; и осью ox. Замечание. Для того, чтобы ввести классы интегрируемых функций введём понятие так называемых сумм Дарбу (итальянский математик). Обозначим: mi – точная нижняя граница f(x) на (xi; xi+1); Mi- точная верхняя граница f(x) на (xi; xi+1); Тогда, если ziÎ[xi; xi+1], то mi£f(zi)£Mi Определение. Суммы вида Замечание. При любом разбиении промежутка [a, b]. любая интегральная сумма будет заключена между верхней и нижней суммами Дарбу.
Теорема. (Условие существования интеграла). Для существования определённого интеграла необходимо и достаточно, чтобы
На основании этой теоремы устанавливаются классы интегрируемых функций. 1. Всякая непрерывная на [a, b] функция интегрируема на этом промежутке. 2. Всякая ограниченная на [a, b] функция, имеющая конечное число точек разрыва интегрируема на этом промежутке. 3. Всякая ограниченная и монотонная на [a, b] функция интегрируема на [a, b], даже если она имеет бесконечно много точек разрыва.
|

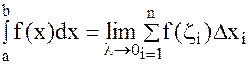
 =m – масса линейного материального стержня [a, b], если f(x)- плотность распределения масс.
=m – масса линейного материального стержня [a, b], если f(x)- плотность распределения масс.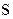 =
= 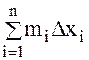 и S=
и S=  MiDxi называются нижней и верхней суммами Дарбу функции f(x) на [a, b].
MiDxi называются нижней и верхней суммами Дарбу функции f(x) на [a, b].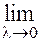 (S-
(S- 


