Определенный интеграл

1.Задачи, приводящие к понятию определенного интеграла.

Задача 1. О массе линейного материального стержня.

Пусть на отрезке [a,b] оси ОХ распределена некоторая масса m, причем

¾¾[¾¾¾¾¾¾¾]¾® x

a b

плотность массы в каждой точке зависит от положения точки, т.е. яв­ляется функцией аргумента х, ρ=ρ(х)-функция распределения массы.

Нам требуется найти массу стержня.

Если бы плотность была постоянной и равна была бы ρ, то масса равна была бы m=ρ(b-a). Но плотность меняется от точки к точке.

Тогда разобьём промежуток [a,b] произвольно на n частей точ­ками x₁, x ₂…..x_n-1;

На каждом элементарном промежутке [x_i;x_i+1] будем считать, что плотность постоянна и равна ρ в точке z_i, где z_iÎ [x_i,x_i+1] тогда масса стержня элементарного промежутка ρ(z_i)(x_i+1 – x_i)=ρ(z_i)∆x_i. Для массы всего cтержня будем иметь приближённую формулу m≈∑ρ(z_i)∆x:

Погрешность этой формулы будет уменьшаться с уменьшением длины элементарного промежутка, λ=max(x_i;x_i+1). За точное значение массы принимают предел полученной суммы при λ →0 т.е.

_n

m=lim år(z_i)Dx_i

^{l®0 i=1}

 

Замечание. Такое определение массы имеет смысл, когда суще­ствует такой предел, и он не зависит ни от числа точек разбиения на элементарные части, ни от способа выбора точек z_i.

Задача 2. (О площади криволинейной трапеции). Найти пло­щадь ограниченную y=f(x), осью OX и x=a; x=b;

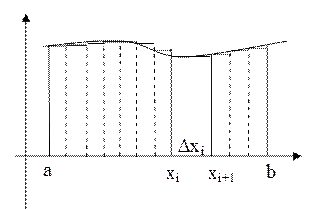
Решение. Разобьём промежуток [a, b] на n частей произвольно.

x₀ =a<x₁<x₂<…x_i<x_i+1<…x_n-1<x_n=b

площадь элементарного прямоугольника S_i=f(x_i)∆x_i. Площадь криволинейной трапеции приближенно равна

_n

S≈∑ f(x_i)∆x_i.

ⁱ⁼¹

Погрешность этой формулы уменьшится, если λ=max(∆x_i)→0. Тогда перейдем к пределу

_n

S=lim å f(x_i)Dx_i

^{l®0 i=1}