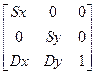Схема преобразования координатных систем
Мы выведем только преобразования координат X. Преобразования координат Y будут выполняться аналогично.
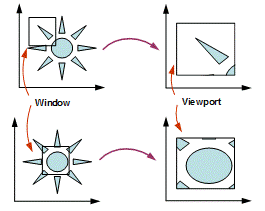
Определим, как найти в поле вывода точку, соответствующую точке, заданной в окне, как показано на рисунке 3.3. Для этого используем простую пропорцию В этой формуле выражение
Рассуждая аналогично, можно получить формулу для координаты Y: И переходя к матричной форме Pv=PwST=PwM [x’ y’ 1] = [x y 1] Обратное преобразование, из поля вывода в окно, нам потребуется для выполнения лабораторных работ. Его необходимо найти самостоятельно. Обратите внимание на то, что прямоугольники, определяющие окно и поле вывода должны быть подобны, т.е. иметь одинаковые пропорции между высотой и шириной. В противном случае масштабирующие коэффициенты по осям x и y будут различны, что приведет к нарушению пропорции всех отображаемых объектов. Посмотрим, как при такой схеме преобразования производится нормализация. Поле вывода нормализующего преобразования задается в NDC. При приведении к диапазону [0..1] определяющие поле вывода точки имеют координаты (0,0) и (1,1). Окно преобразование задается в мировых координатах таким образом, что бы сформировался квадрат, полностью включающий в себя модель. Полученный в данном преобразовании коэффициент масштабирования учитывается при расчете общего масштаба модели при визуализации.
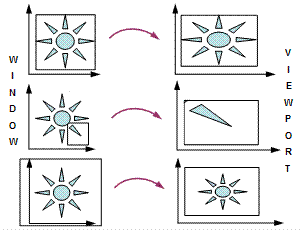
Рисунок 3.4 Изменения изображения при модификации окна. Остановим наше внимание на свойствах преобразования. Для упрощения примеров зафиксируем размер поля вывода и будем производить изменения окна, как это показано на рисунке 3.4. Мы специально нарушили подобие окна и поля вывода, чтобы показать возникающие искажения. При переносе окна мы видим различные фрагменты сцены, т.е. происходит «прокрутка» изображения в поле вывода. При изменении размеров окна меняется масштаб выводимого изображения, естественно при этом изменяется видимая часть фрагмента. При увеличении окна мы видим больший фрагмент изображения, но с меньшим масштабом. И наоборот, при уменьшении окна масштаб увеличивается, и мы видим меньший фрагмент, но более детально. Подобным образом в графических системах реализуется функция изменения масштаба (Zoom или Лупа).
|

 Рисунок 3.3 Схема преобразования.
Рисунок 3.3 Схема преобразования.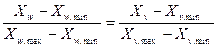 . Откуда, выразим Хvp - координату поля вывода, через Хw - координату окна
. Откуда, выразим Хvp - координату поля вывода, через Хw - координату окна 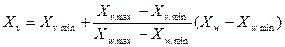
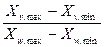 можно рассматривать как масштабирующий коэффициент, так как в рамках одного преобразования координаты точек, определяющих окно и поле вывода, являются постоянными (константы). Следовательно,
можно рассматривать как масштабирующий коэффициент, так как в рамках одного преобразования координаты точек, определяющих окно и поле вывода, являются постоянными (константы). Следовательно, 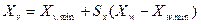 . Открывая скобки и перегруппировывая получаем:
. Открывая скобки и перегруппировывая получаем: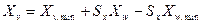 ,
,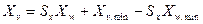 . Очевидно, что
. Очевидно, что 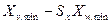 формируют простой перенос. Обозначив его как Тх, приходим к конечной формуле
формируют простой перенос. Обозначив его как Тх, приходим к конечной формуле 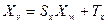 .
. .
.