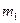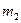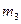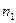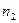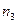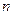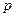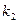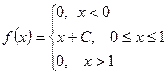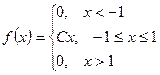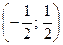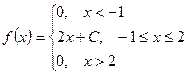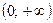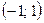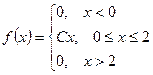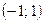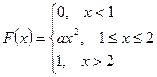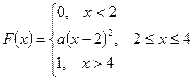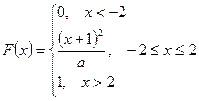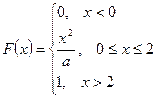ВЕРОЯТНОСТЬ И СТАТИСТИКА.
Задания для выполнения контрольной работы Решите самостоятельно следующие задачи. Данные своей 1. В урне N билетов. Из них М выигрышных. Какова вероятность того, что первый вынутый билет окажется выигрышным? 2. Биатлонист стреляет в мишень. Мишень - круг радиуса R см. Биатлонист попадает в мишень с вероятностью 1. Попадание в любую точку мишени равновероятно. Необходимо попасть в круг радиуса R1 см. 3. Имеется собрание сочинений из N томов некоего автора. Все Nтомов расставляются на книжной полке случайным образом. Какова вероятность того, что тома расположатся в порядке 1, 2,……, Nили N, N – 1,…,1?
4. Имеется собрание сочинений из N томов некоего автора. На
5. Имеется собрание сочинений из N томов некоего автора. На
6. Три стрелка стреляют по мишени. Предполагается, что события попадания в мишень для стрелков независимы и вероятности попадания стрелков в мишень равны p1, p2, р3. Какова вероятность того, что: а) все три выстрела окажутся успешными; б) хотя бы один из трёх выстрелов окажется успешным; в) точно один выстрел окажется успешным, два неуспешными?
7. Экзамен сдавали студенты трех групп, причем в
8. Вероятность наступления некоторого события в каждом из n независимых испытаний равна p. Определить вероятность того, что число m наступлений события удовлетворяет следующему неравенству. Вариант 1 – 4: Варианты 5,6,7: Варианты 8,9,10:
9. Вероятность детали быть бракованной равна р. Произведено 1000 деталей. Какова вероятность того, что в этой партии точно 2 бракованных детали? Более 2?
10. Случайная величина X задана рядом распределения.
Найти математическое ожидание MX, дисперсию DX, σх вероятности Р( X < 0), Р (X > 0), найти функцию распределения, построить ее график. У = 2Х + b. Найти математическое ожидание MY, дисперсию DY. 11. Футболист бьёт N раз пенальти. Вероятность забить при одном ударе - р. Какова вероятность того, что будет забито 3 мяча? Более 2? Найти математическое ожидание MX, дисперсию DX. 12. Количество X принимаемых за час звонков по домашнему телефону имеет распределение Пуассона. Среднее количество принимаемых за час звонков - λ. Какова вероятность, что будет принято 3 звонка? Более 2? Найти математическое ожидание MX, дисперсию DX. 13. Вариант 1 – 5: Непрерывная случайная величина Х задана плотностью распределения вероятностей Вариант 6 – 10: Непрерывная случайная величина Х задана функцией распределения 14. Случайная величина Х- время ожидания дождя в сутках - имеет равномерное распределение на отрезке [0,N]. Найти математическое ожидание MX, дисперсию DX, вероятности Р(Х< 5), Р(Х> 3). 15. Вероятность безотказной работы прибора в течение х часов равна е-λx. Найти математическое ожидание MX- среднюю наработку на отказ и вероятность безотказной работы прибора в течение 100 ч.
а = MX, σ =
Данные к задачам 1-6
Данные к задачам 9,10,11,12,14,15,16.
Задача 7
Задача 8.
Задача 13.
|

 -й группе учатся
-й группе учатся  % студентов
% студентов  . Вероятность сдать экзамен на положительную оценку для студента
. Вероятность сдать экзамен на положительную оценку для студента  %. Наудачу выбранный студент экзамен не сдал. Определить вероятность того, что этот студент из
%. Наудачу выбранный студент экзамен не сдал. Определить вероятность того, что этот студент из 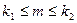
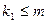
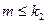
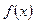 . Найти: С, М(Х), D(Х), вероятность попадания случайной величины в заданный интервал.
. Найти: С, М(Х), D(Х), вероятность попадания случайной величины в заданный интервал. . Найти: а, f(x), М(Х), D(Х).
. Найти: а, f(x), М(Х), D(Х). 16. Случайная величина Х имеет нормальное распределение N(a,σ)
16. Случайная величина Х имеет нормальное распределение N(a,σ)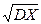 - среднеквадратическое отклонение. Найти P(Х< 1), P(-1 <Х< 1), P(-5 <Х< 5), P(-σ <X- a < σ), Р(-2σ < X - а < 2σ), Р(-Зσ < X - а < Зσ).
- среднеквадратическое отклонение. Найти P(Х< 1), P(-1 <Х< 1), P(-5 <Х< 5), P(-σ <X- a < σ), Р(-2σ < X - а < 2σ), Р(-Зσ < X - а < Зσ).