Переходные процессы в RLC-цепях
Если в момент времени t = 0 к RLC -цепи (рис. 4.5) подключить источник с ЭДС, равной
Рис. 4.5
Запишем для указанного на рис. 4.5 контура уравнение по второму закону Кирхгофа:
Решая уравнение (4.3) относительно
где
Графики зависимостей Степень затухания в контуре принято характеризовать величиной, называемой логарифмическим декрементом затухания θ:
где
Рис. 4.6
Важной характеристикой контура является добротность Q, характеризующая степень убывания энергии в контуре с течением времени. Добротность связана с логарифмическим декрементом соотношением
При малых значениях активного сопротивления R, когда
где
Отметим, что при
При переключении ключа П из положения 1 в положение 2 амплитуда колебаний силы тока в цепи вновь возрастает, при этом законы изменения напряжения в контуре аналогичны описанным выше.
|
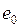(переключатель П в положении 1), то в цепи возникнут затухающие колебания.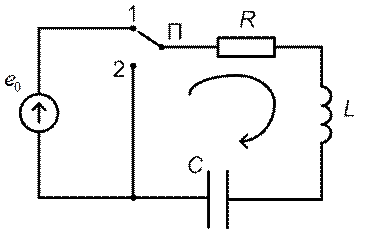
,
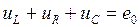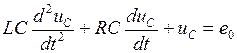. (4.3)
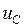, получим зависимость падания напряжения на конденсаторе от времени:
,
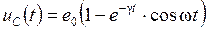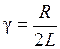- коэффициент затухания в контуре,
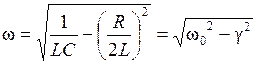- частота собственных затухающих колебаний в RLC -контуре,
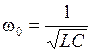- частота собственных незатухающих колебаний в контуре при R = 0.
, 
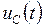приведены на рис. 4.6.
,
, 
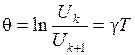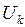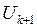- значения напряжение на конденсаторе, соответствующие двум соседним максимумам колебаний.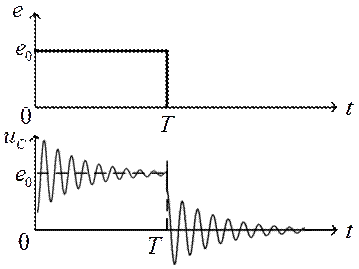
.
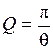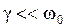, для добротности и частоты собственных колебаний можно записать:
, 
,
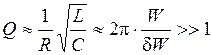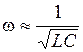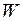- энергия, запасённая в контуре,
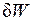- уменьшение этой энергии за период колебания 
.
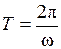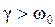(затухание велико) зависимость 
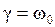, называют критическим:
.
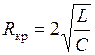