Пусть в момент времени t = 0 к RL -цепи (рис. 4.3) подключили источник с ЭДС, равной 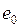 (переключатель П в положении 1).
(переключатель П в положении 1).
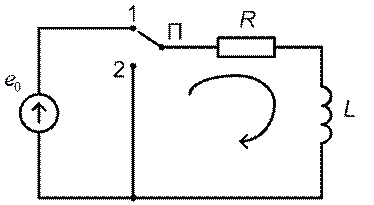
Рис. 4.3
Запишем для указанного на рис. 4.3 контура уравнение по второму закону Кирхгофа:
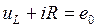 ,
,
 . (4.2)
. (4.2)
Решив дифференциальное уравнение (4.2) относительно  , учитывая при этом начальное условие, вытекающее из законов коммутации,
, учитывая при этом начальное условие, вытекающее из законов коммутации, 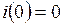 , и вынужденную составляющую решения
, и вынужденную составляющую решения 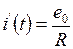 , получим
, получим
 ,
,
 ,
,
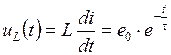 .
.
Константа 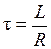 , имеющая размерность времени и характеризующая скорость изменения тока в цепи, называется постоянной времени RL -цепи, или временем релаксации.
, имеющая размерность времени и характеризующая скорость изменения тока в цепи, называется постоянной времени RL -цепи, или временем релаксации.
В момент времени 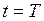 переключатель П переводится в положение 2 и тем самым источник ЭДС отключается от цепи.
переключатель П переводится в положение 2 и тем самым источник ЭДС отключается от цепи.
Решая дифференциальное уравнение (4.2) относительно  , полагая
, полагая  , учитывая при этом начальное условие, вытекающее из законов коммутации,
, учитывая при этом начальное условие, вытекающее из законов коммутации, 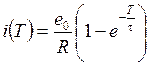 , и вынужденную составляющую решения
, и вынужденную составляющую решения 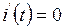 , находим для
, находим для 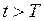
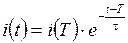 ,
,
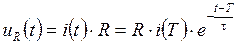 ,
,
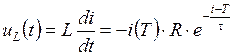 .
.
Графики зависимостей  ,
,  ,
,  для рассмотренного процесса приведены на рис. 4.4.
для рассмотренного процесса приведены на рис. 4.4.

Рис. 4.4

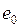 (переключатель П в положении 1).
(переключатель П в положении 1).
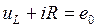 ,
, . (4.2)
. (4.2) , учитывая при этом начальное условие, вытекающее из законов коммутации,
, учитывая при этом начальное условие, вытекающее из законов коммутации, 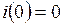 , и вынужденную составляющую решения
, и вынужденную составляющую решения 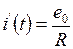 , получим
, получим ,
, ,
,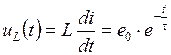 .
.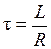 , имеющая размерность времени и характеризующая скорость изменения тока в цепи, называется постоянной времени RL -цепи, или временем релаксации.
, имеющая размерность времени и характеризующая скорость изменения тока в цепи, называется постоянной времени RL -цепи, или временем релаксации.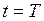 переключатель П переводится в положение 2 и тем самым источник ЭДС отключается от цепи.
переключатель П переводится в положение 2 и тем самым источник ЭДС отключается от цепи. , учитывая при этом начальное условие, вытекающее из законов коммутации,
, учитывая при этом начальное условие, вытекающее из законов коммутации, 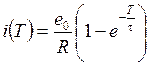 , и вынужденную составляющую решения
, и вынужденную составляющую решения 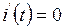 , находим для
, находим для 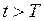
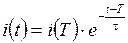 ,
,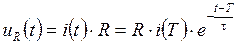 ,
,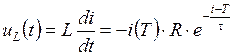 .
. ,
,  ,
,  для рассмотренного процесса приведены на рис. 4.4.
для рассмотренного процесса приведены на рис. 4.4.



