Энергетические характеристики
Интенсивность звука. Акустические колебания – частный случай механических колебаний, поэтому мгновенное значение акустической мощности, как и в механике, определяется произведением мгновенных значений силы Если в рассматриваемой точке звукового поля мгновенные значения давления и скорости колебаний имеют одинаковый знак, то вектор Умова направлен в сторону распространения волны, т. е. энергия движется от источника звука; если они имеют разные знаки, то – против движения волны, т. е. энергия движется к источнику звука. Последнее возможно только при наличии сдвига фаз между звуковым давлением и скоростью колебаний и означает наличие реактивной составляющей мощности. Наибольший интерес представляет среднее значение удельной мощности колебаний
где Для синусоидальных колебаний интенсивность звука
где Интенсивность звука представляет собой активную составляющую удельной мощности звуковых колебаний. Реактивная составляющая мощности колебаний непрерывно колеблется в звуковом поле то в сторону распространения волны, то в обратную. Эта часть мощности колебаний представляет собой запас энергии в звуковом поле аналогично запасу энергии в электрическом и магнитном полях электрического тока [4]. Плотность энергии. Среднее количество звуковой энергии, приходящееся на единицу объема, называют плотностью энергии. Единицей плотности энергии в системе СИ является Для определения связи между интенсивностью звука и плотностью энергии выделим объем по направлению движения волны (рис. 1.2). Энергия, находившаяся в нем к моменту рассмотрения и равная Так как согласно определению интенсивность звука
а с учетом (1.14) находим
|

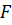 и скорости колебаний
и скорости колебаний  , т. е.
, т. е. 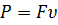 . Если имеется в виду сила, действующая на единицу площади, т. е. давление, то следует говорить об удельной мощности колебаний
. Если имеется в виду сила, действующая на единицу площади, т. е. давление, то следует говорить об удельной мощности колебаний 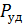 (называемой вектором Умова), равной произведению звукового давления
(называемой вектором Умова), равной произведению звукового давления 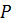 и скорости колебаний
и скорости колебаний 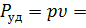
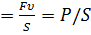 .
.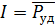 , распространяющейся в положительном направлении, т. е. среднее значение потока энергии через единицу площади, двигающегося от источника звука к возможному приемнику звука. Это среднее значение называют интенсивностью или силой звука. Итак, интенсивностью звука называют (среднее) количество звуковой энергии, проходящей в единицу времени через единицу площади, перпендикулярной направлению распространения звуковой волны. В системе СИ единица интенсивности
, распространяющейся в положительном направлении, т. е. среднее значение потока энергии через единицу площади, двигающегося от источника звука к возможному приемнику звука. Это среднее значение называют интенсивностью или силой звука. Итак, интенсивностью звука называют (среднее) количество звуковой энергии, проходящей в единицу времени через единицу площади, перпендикулярной направлению распространения звуковой волны. В системе СИ единица интенсивности 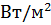 . Для периодических и сложных звуков интенсивность выражается формулами:
. Для периодических и сложных звуков интенсивность выражается формулами: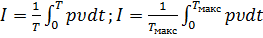 , (1.13)
, (1.13) ;
; 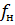 – частота наиболее низкочастотной составляющей звука.
– частота наиболее низкочастотной составляющей звука.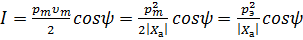 , (1.14)
, (1.14) и
и 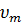 – амплитуды звукового давления и скорости колебаний;
– амплитуды звукового давления и скорости колебаний; 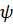 – сдвиг фаз между ними;
– сдвиг фаз между ними; 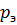 – действующее значение звукового давления;
– действующее значение звукового давления; 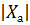 – модуль акустического сопротивления.
– модуль акустического сопротивления.
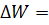
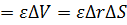 , выйдет из него за время
, выйдет из него за время  , где
, где 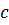 – скорость звука;
– скорость звука; 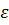 – плотность энергии. Поток этой энергии
– плотность энергии. Поток этой энергии 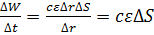 .
.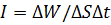 , то, подставляя в него предыдущее выражение, получаем
, то, подставляя в него предыдущее выражение, получаем 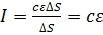 , откуда
, откуда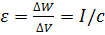 , (1.15)
, (1.15)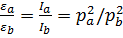 . (1.16)
. (1.16)


