Плоская волна
Фронт плоской волны представляет собой плоскость. Согласно определению фронта волны звуковые лучи пересекают его под прямым углом, поэтому в плоской волне они параллельны между собой. Так как поток энергии при этом не расходится, интенсивность звука не должна была бы уменьшаться с удалением от источника звука. Тем не менее она уменьшается из-за молекулярного затухания, вязкости среды, запыленности ее, рассеяния и т. п. потерь. Однако эти потери так малы, что с ними можно не считаться при распространении волны на небольшие расстояния. Поэтому обычно полагают, что интенсивность звука в плоской волне не зависит от расстояния до источника звука. Поскольку Выведем основные уравнения для плоской волны. Уравнение (1.8) имеет вид, так как Подставляя звуковое давление в уравнение движения (1.5) и интегрируя во времени, получим скорость колебаний Из этих выражений находим удельное акустическое сопротивление (1.10) для плоской волны:
Для нормального атмосферного давления и температуры
|

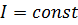 , то амплитуды звукового давления и скорости колебаний тоже не зависят от этого расстояния:
, то амплитуды звукового давления и скорости колебаний тоже не зависят от этого расстояния:  ;
;  .
. . Частное решение волнового уравнения для плоской волны, распространяющейся в положительном направлении, имеет вид
. Частное решение волнового уравнения для плоской волны, распространяющейся в положительном направлении, имеет вид 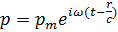 , где
, где  – амплитуда звукового давления;
– амплитуда звукового давления;  – угловая частота колебаний;
– угловая частота колебаний;  – волновое число.
– волновое число. , где
, где 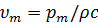 – амплитуда скорости колебаний.
– амплитуда скорости колебаний. . (1.17)
. (1.17)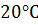 акустическое сопротивление
акустическое сопротивление 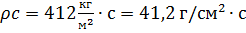 . Акустическое сопротивление для плоской волны определяется только скоростью звука и плотностью среды и является активным, вследствие чего давление и скорость колебаний находятся в одинаковой фазе, т. е.
. Акустическое сопротивление для плоской волны определяется только скоростью звука и плотностью среды и является активным, вследствие чего давление и скорость колебаний находятся в одинаковой фазе, т. е.  , поэтому интенсивность звука
, поэтому интенсивность звука 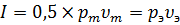 где
где 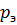 и
и 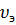 – действующие значения звукового давления и скорости колебаний. Подставляя в это выражение (1.17), получаем наиболее часто используемое выражение для определения интенсивности звука
– действующие значения звукового давления и скорости колебаний. Подставляя в это выражение (1.17), получаем наиболее часто используемое выражение для определения интенсивности звука . (1.18)
. (1.18)


