Звуковое давление. Положим, что давление среды в отсутствие звуковых колебаний равно 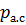 , это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения – меньше. Разность между мгновенным давлением
, это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения – меньше. Разность между мгновенным давлением  и статическим
и статическим 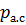 в той же точке среды, т. е. переменная составляющая давления (часто звуковое давление называют избыточным давлением среды, такое название ассоциируется с положительным приращением давления), называется звуковым давлением
в той же точке среды, т. е. переменная составляющая давления (часто звуковое давление называют избыточным давлением среды, такое название ассоциируется с положительным приращением давления), называется звуковым давлением 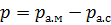 .
.
Звуковое давление – величина знакопеременная. Давление 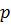 – сила, действующая на единицу площади, т. е.
– сила, действующая на единицу площади, т. е.  . Поэтому за единицу давления в системе СИ принимают ньютон на квадратный метр
. Поэтому за единицу давления в системе СИ принимают ньютон на квадратный метр 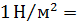
 (паскаль)
(паскаль) 
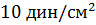 . В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление.
. В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление.
Скорость колебаний. Если давления неодинаковы в соседних точках среды, то ее частицы стремятся сместиться в сторону минимального давления. При знакопеременной разности давлений возникает колебательное движение частиц среды около своего статического положения. Скорость колебаний этих частиц  , где
, где 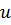 – смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука – постоянная величина для данной среды и метеорологических условий, а скорость колебаний – переменная, причем если частица среды
– смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука – постоянная величина для данной среды и метеорологических условий, а скорость колебаний – переменная, причем если частица среды
перемещается по направлению распространения волны, то скорость считают положительной, а при обратном перемещении частицы – отрицательной.

Рисунок 1.2 – Вывод уравнения движения
Определим связь между звуковым давлением и скоростью колебаний. Возьмем элементарный объем, заключенный между фронтами волн, находящимися на расстоянии  друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений
друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений 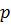 и
и  , следовательно, испытываемая ею сила
, следовательно, испытываемая ею сила  , где
, где 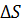 – площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции
– площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции 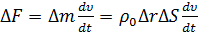 , где
, где  – масса среды, заключенной в этом объеме;
– масса среды, заключенной в этом объеме; 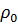 – средняя плотность среды. Так как в вещании и связи имеют дело с изменением плотности среды не более чем на 0,1%, в дальнейшем индекс у
– средняя плотность среды. Так как в вещании и связи имеют дело с изменением плотности среды не более чем на 0,1%, в дальнейшем индекс у 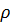 опускаем. Приравнивая обе силы, получаем
опускаем. Приравнивая обе силы, получаем 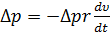 . Так как
. Так как 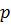 и
и  зависят как от координат, так и от времени, то, переходя к производным, имеем
зависят как от координат, так и от времени, то, переходя к производным, имеем
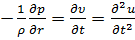 . (1.5)
. (1.5)
Это уравнение называется уравнением движения среды.
Деформация идеальной (невязкой) газообразной среды, появляющаяся при распространении в ней звуковой волны, является адиабатической, так как звуковые процессы происходят быстро, без теплообмена. Поэтому эти процессы подчиняются закону Бойля-Мариотта с поправкой Пуассона.
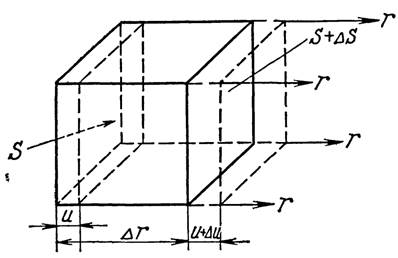
Рисунок 1.3 – Вывод уравнения непрерывности
 , где
, где  – показатель адиабаты для воздуха
– показатель адиабаты для воздуха 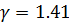 . Выделяем элементарный объём
. Выделяем элементарный объём 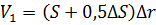 (рис. 1.3) как и в предыдущем случаи. В статистическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объём непрерывно изменяется. Положим, что в некоторый момент частицы среды слева будут смещены на величину
(рис. 1.3) как и в предыдущем случаи. В статистическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объём непрерывно изменяется. Положим, что в некоторый момент частицы среды слева будут смещены на величину 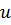 , а справа – на величину
, а справа – на величину  , тогда, при условии непрерывности среды этот объем
, тогда, при условии непрерывности среды этот объем  Разделим обе части выражения на
Разделим обе части выражения на 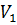 и в правой части заменим
и в правой части заменим 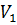 на
на 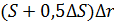 .
.
При пренебрежении членами второго порядка малости получим 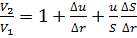 . Заметим, что последний член в этом выражении обусловлен расхождением (дивергенцией) франта волны.
. Заметим, что последний член в этом выражении обусловлен расхождением (дивергенцией) франта волны.
При звуковых колебаниях полное давление газообразной среды  , где
, где 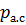 – статическое давление;
– статическое давление; 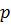 – звуковое давление. Следовательно,
– звуковое давление. Следовательно, 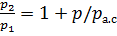 . Подставив
. Подставив 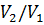 и
и 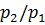 в уравнение за кона Пуассона, получим
в уравнение за кона Пуассона, получим 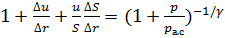 . Как указывалось ранее
. Как указывалось ранее  , поэтому
, поэтому 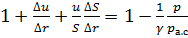 или
или 
 Переходя к производным, находим
Переходя к производным, находим
 . (1.6)
. (1.6)
Это уравнение называют уравнением состояния среды. Если это уравнение продифференцировать дважды по  и переставить порядок дифференцирования, то получим
и переставить порядок дифференцирования, то получим 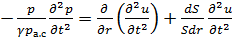 . Подставляя в него производную
. Подставляя в него производную 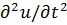 из уравнения движения (1.5), получим уравнение для звукового давления
из уравнения движения (1.5), получим уравнение для звукового давления  . Заменяя в нем
. Заменяя в нем
 , (1.7)
, (1.7)
получим
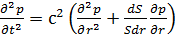 . (1.8)
. (1.8)
Это уравнение называют волновым уравнением Вебстера.
Общее волновое уравнение имеет вид
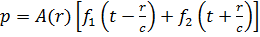 . (1.9)
. (1.9)
Если в первую составляющую решения вместо  подставить
подставить 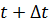 , то для неизменности аргумента следует вместо
, то для неизменности аргумента следует вместо  подставить
подставить 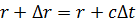 . Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений
. Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений  , вторая – в обратном направлении. Из тех же данных следует, что
, вторая – в обратном направлении. Из тех же данных следует, что 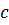 – скорость распространения волны, так как
– скорость распространения волны, так как  . Таким образом, скорость звука
. Таким образом, скорость звука 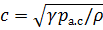 , т. е. определяется статическим давлением среды и ее плотностью [2].
, т. е. определяется статическим давлением среды и ее плотностью [2].
Акустическое сопротивление. Разность давлений является причиной движения частиц среды, а разность потенциалов – причиной движения электрических зарядов. Скорость колебаний частиц среды аналогична скорости движения зарядов – силе тока. Аналогично электрическому сопротивлению введено понятие волнового акустического сопротивления. Удельным волновым акустическим сопротивлением называют отношение звукового давления к скорости колебаний. Удельным оно называется потому, что представляет собой сопротивление для единицы площади фронта волны. Для краткости его часто называют акустическим сопротивлением
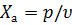 . (1.10)
. (1.10)
Акустическое сопротивление определяется прежде всего свойствами среды. В ряде случаев оно зависит от частоты колебаний и от формы фронта волны. В общем виде оно комплексное:
 , (1.11)
, (1.11)
где  и
и 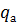 – активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения
– активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения
 . (1.12)
. (1.12)

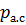 , это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения – меньше. Разность между мгновенным давлением
, это давление называют статическим. При прохождении звуковой волны давление в каждой точке среды будет непрерывно изменяться: в моменты сгущения частиц оно больше статического, а в моменты разрежения – меньше. Разность между мгновенным давлением  и статическим
и статическим 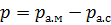 .
.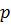 – сила, действующая на единицу площади, т. е.
– сила, действующая на единицу площади, т. е.  . Поэтому за единицу давления в системе СИ принимают ньютон на квадратный метр
. Поэтому за единицу давления в системе СИ принимают ньютон на квадратный метр 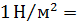
 (паскаль)
(паскаль) 
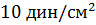 . В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление.
. В системах связи и вещания имеют дело с звуковыми давлениями, по амплитуде, не превышающими 100 Па, т. е., по крайней мере, в 1000 раз меньше, чем нормальное атмосферное давление. , где
, где 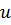 – смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука – постоянная величина для данной среды и метеорологических условий, а скорость колебаний – переменная, причем если частица среды
– смещение частиц. Скорость колебаний обычно измеряют в метрах или сантиметрах в секунду. Не следует путать эту скорость со скоростью звука. Скорость звука – постоянная величина для данной среды и метеорологических условий, а скорость колебаний – переменная, причем если частица среды
 друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений
друг от друга, с боковыми поверхностями, расположенными вдоль звуковых лучей (рис. 1.2). Как видно из рисунка, среда в этом объеме находится под действием разности давлений  , следовательно, испытываемая ею сила
, следовательно, испытываемая ею сила  , где
, где 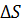 – площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции
– площадь, выделенная на поверхности фронта волны. С другой стороны, по второму закону Ньютона сила инерции 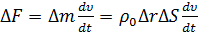 , где
, где  – масса среды, заключенной в этом объеме;
– масса среды, заключенной в этом объеме; 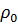 – средняя плотность среды. Так как в вещании и связи имеют дело с изменением плотности среды не более чем на 0,1%, в дальнейшем индекс у
– средняя плотность среды. Так как в вещании и связи имеют дело с изменением плотности среды не более чем на 0,1%, в дальнейшем индекс у 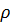 опускаем. Приравнивая обе силы, получаем
опускаем. Приравнивая обе силы, получаем 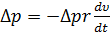 . Так как
. Так как  зависят как от координат, так и от времени, то, переходя к производным, имеем
зависят как от координат, так и от времени, то, переходя к производным, имеем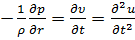 . (1.5)
. (1.5)
 , где
, где  – показатель адиабаты для воздуха
– показатель адиабаты для воздуха 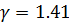 . Выделяем элементарный объём
. Выделяем элементарный объём 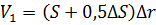 (рис. 1.3) как и в предыдущем случаи. В статистическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объём непрерывно изменяется. Положим, что в некоторый момент частицы среды слева будут смещены на величину
(рис. 1.3) как и в предыдущем случаи. В статистическом состоянии в нем находится определенное количество частиц среды. При звуковых колебаниях занимаемый ими объём непрерывно изменяется. Положим, что в некоторый момент частицы среды слева будут смещены на величину  , тогда, при условии непрерывности среды этот объем
, тогда, при условии непрерывности среды этот объем  Разделим обе части выражения на
Разделим обе части выражения на 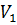 и в правой части заменим
и в правой части заменим 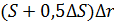 .
.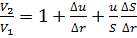 . Заметим, что последний член в этом выражении обусловлен расхождением (дивергенцией) франта волны.
. Заметим, что последний член в этом выражении обусловлен расхождением (дивергенцией) франта волны. , где
, где 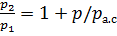 . Подставив
. Подставив 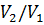 и
и 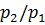 в уравнение за кона Пуассона, получим
в уравнение за кона Пуассона, получим 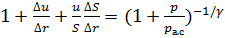 . Как указывалось ранее
. Как указывалось ранее  , поэтому
, поэтому 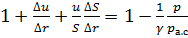 или
или 
 Переходя к производным, находим
Переходя к производным, находим . (1.6)
. (1.6) и переставить порядок дифференцирования, то получим
и переставить порядок дифференцирования, то получим 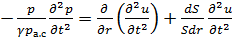 . Подставляя в него производную
. Подставляя в него производную 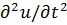 из уравнения движения (1.5), получим уравнение для звукового давления
из уравнения движения (1.5), получим уравнение для звукового давления  . Заменяя в нем
. Заменяя в нем , (1.7)
, (1.7)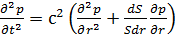 . (1.8)
. (1.8)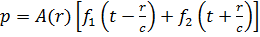 . (1.9)
. (1.9)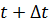 , то для неизменности аргумента следует вместо
, то для неизменности аргумента следует вместо  подставить
подставить 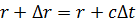 . Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений
. Следовательно, первая составляющая представляет собой волну, распространяющуюся в сторону положительных значений 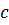 – скорость распространения волны, так как
– скорость распространения волны, так как  . Таким образом, скорость звука
. Таким образом, скорость звука 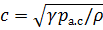 , т. е. определяется статическим давлением среды и ее плотностью [2].
, т. е. определяется статическим давлением среды и ее плотностью [2].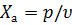 . (1.10)
. (1.10) , (1.11)
, (1.11) и
и 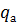 – активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения
– активная и реактивная составляющие акустического сопротивления. Наличие реактивной составляющей свидетельствует о том, что между звуковым давлением и скоростью колебаний есть сдвиг фаз. Этот сдвиг определяется из соотношения . (1.12)
. (1.12)


