Методические указания. При изучении дифференциального уравнения теплопроводности Фурье обратить внимание, что его вывод основан на законе сохранения энергии
При изучении дифференциального уравнения теплопроводности Фурье обратить внимание, что его вывод основан на законе сохранения энергии, на законе теплопроводности Фурье и на допущении о постоянном значении коэффициента теплопроводности, которые и определяют существо этого уравнения и область его применения. В исходном уравнении [1, с.16 (1-22)] допущено отступление от принятых в книге обозначений: вместо
Вопросы для самопроверки. 1.1. Могут ли изотермические поверхности пересекаться? (Да, нет). 1.2. Могут ли изотермические поверхности быть замкнутыми? (Да, нет). 1.3. Из двух противоположных утверждений (gradt 1.4. Достаточно ли знать градиенты температурного поля, чтобы определить разность температур между точками поля? (Да, нет). 1.5. Достаточно ли знать продолжительность нагрева и количество теплоты, подведенной за это время к телу произвольных размеров, чтобы определить плотность теплового потока на поверхности тела? (Да, нет). 1.6. Могут ли быть одинаковыми истинная и средняя плотности теплового потока? (Да, нет). 1.7. Может ли средняя объемная мощность внутренних источников теплоты быть равной дивергенции потока теплоты? (Да, нет). 1.8. Могут ли быть выражены в одинаковых единицах плотность теплового потока и объемная мощность внутренних источников теплоты? (Да, нет). 1.9. Возможна ли дивергенция потоков теплоты при отсутствии внутренних источников (приемников) теплоты? (Да, нет). 1.10. Можно ли рассматривать дифференциальное уравнение теплопроводности Фурье как одну из форм закона сохранения энергии? (Да, нет). 1.11. Можно ли применить уравнение Лапласа к анализу процессов нестационарной теплопроводности? (Да, нет). 1.12. Входят ли физические параметры тела в состав условий однозначности, необходимых для решения дифференциального уравнения теплопроводности? (Да, нет).
|

 d
d  и d
и d 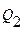 следовало бы написать
следовало бы написать  и
и 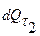 , а вместо
, а вместо 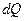 – величину dU или dH.
– величину dU или dH.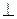 изотерме; gradt êê
изотерме; gradt êê  изотерме) является ли правильным именно второе? (Да, нет).
изотерме) является ли правильным именно второе? (Да, нет).


