Контрольная работа 1
Вопросы
1.Пользуясь справочными данными, например в учебной литературе [1] или [2], приведите два-три наименования материалов с низким коэффициентом теплопроводности. Укажите область применения этих материалов. 2.Пользуясь справочными данными, например в учебной литературе [1] или [2], приведите два-три наименования материалов с высоким коэффициентом теплопроводности. Укажите область применения этих материалов. 3.Пользуясь справочными данными, например в учебной литературе [2], приведите два-три наименования огнеупорных материалов. Приведите их основные характеристики и укажите области их применения. 4.Пользуясь справочными данными, например в учебной литературе [2], приведите два-три наименования изоляционных материалов и изделий с температурной стойкостью не выше 400-420°С. Укажите области их применения. 5.Пользуясь справочными данными, например в учебной литературе [2],приведите два-три наименования изоляционных материалов и изделий с температурной стойкостью до 600°С. Укажите область их применения. 6.Пользуясь справочными данными, например в учебной литературе [2], приведите два-три наименования изоляционных материалов и изделий с предельно высокой температурной стойкостью. Укажите область их применения. 7.Пользуясь справочными данными, например в учебной литературе [2], приведите два-три наименования материалов с низкой плотностью. Приведите их основные характеристики. Сравните их коэффициенты теплопроводности с коэффициентом теплопроводности воздуха. 8.Пользуясь справочными данными, например в учебной литературе [2], выберите наименование и марку стали, у которой теплопроводность мало зависит от температуры, и марку стали, у которой теплопроводность, наоборот, сильно зависит от температуры. Представьте обе зависимости в виде графика. 9.Пользуясь справочными данными, например в учебной литературе [2], выберите несколько металлов или сплавов с минимальным и максимальными значениями коэффициентов теплопроводности при 20°С. 10.Пользуясь справочными данными, например в учебной литературе [2], выберите два материала: один —с ростом, другой —с убыванием коэффициента теплопроводности в зависимости от температуры. Представьте эти зависимости в виде графика. 11.Дайте понятие температурного поля. Назовите характеристики температурного поля. Приведите примеры. 12.Укажите, в чем состоят условия, характеризующие наряду с формой, размерами и физическими параметрами однозначность стационарного теплообмена твердого тела. 13.Опишите одномерное плоское температурное поле. Дайте его аналитическое и графическое изображение. Приведите примеры. 14.Опишите одномерное сферическое температурное поле. Дайте его аналитическое и графическое изображение. Приведите примеры. 15.Укажите основные способы и приведите примеры графического изображения температурного поля. 16.Опишите одномерное цилиндрическое температурное поле. Дайте его аналитическое и графическое изображение. Приведите примеры. 17.Как изменяется градиент температуры по толщине цилиндрической стенки при стационарном тепловом потоке? Обоснуйте пояснения графиками распределения температуры по толщине цилиндрической стенки в двух случаях: а) теплота подводится к внутренней стенке; б) теплота подводится к стенке снаружи. 18.Дайте объяснения понятиям: тепловой поток, плотность теплового потока, линейная плотность потока; приведите их единицы. 19.Какую роль играет коэффициент теплопроводности в расчете теплопроводности твердых тел? Приведите числовые значения этого коэффициента для серебра, нержавеющей стали, бетона, минеральной ваты и воздуха при нормальных условиях. 20.Сформулируйте закон теплопроводности Фурье. Дайте пояснения к величинам, входящим в аналитическое выражение закона; приведите единицы этих величин. 21.Сформулируйте закон теплоотдачи Ньютона — Рихмана. Дайте пояснения к величинам, входящим в аналитическое выражение закона; приведите единицы этих величин. 22. В какой мере должна быть отдалена от поверхности точка, в которой фиксируется температура жидкости в соответствии с законом Ньютона — Рихмана? Проиллюстрируйте графиком изменение температуры жидкости вблизи тепло-oтдающей поверхности. 23.Что такое частное и общее термическое сопротивление? Как они взаимосвязаны? Как определяется перепад температуры при тепловом потоке через термическое сопротивление? 24. Изобразите графически распределение температуры в двухслойной стенке для случаи. 25. Изобразите графически распределение температуры в двухслойной стенке для случая 26. Как определяют термические сопротивления стенки и теплоотдающей поверхности в случаях плоской и цилиндрической стенок? Приведите единицы. 27. Что такое коэффициент теплопередачи? Каковы его выражения в случае плоской и цилиндрической стенки? Укажите единицы. 28. Что такое эквивалентный коэффициент теплопроводности многослойной плоской стенки? Каковы его единицы и какова взаимосвязь с термическим сопротивлением многослойной стенки? 29.Почему стенка кипятильной трубки котлоагрегата имеет со стороны газов температуру, значительно отличающуюся от температуры газов, а со стороны водытемпературу, близкую к температуре воды? 30. Изобразите графически характер распределения температуры в плоской стенке если коэффициент теплопроводности: а) увеличивается с ростом температуры; б) уменьшается с ростом температуры. Поясните различие между графиками 31. Не приводя вывода в целом, укажите, на каких двух основных законах базируется дифференциальное уравнение теплопроводности Фурье. 32. Опишите дифференциальное уравнение теплопроводности Фурье, дайте анализ физического или геометрическою смысла членов уравнения — производной по времени коэффициента температуропроводности, оператора Лапласа и производительности внутренних источников теплоты. Приведите их единицы. 33.Покажите к какому виду приводится оператор Лапласа в случае одномерного плоского,одномерного цилиндрического и одномерного сферического полей. 34.Каковы условия однозначности (краевые условия)? С какой целью они присоединяются к дифференциальному уравнению теплопроводности? 35.Каковы граничные условия третьего рода.'' 36.Для чего к дифференциальному уравнению присоединяются начальные и граничные условия? Перечислите три способа задания граничных условий? 37.Что характеризует собой коэффициент температуропроводности? Выведите его единицу, используя дифференциальное уравнение теплопроводности Фурье. 38.Какие известны способы задания граничных условий для дифференциального уравнения теплопроводности? 39.Используя дифференциальное уравнение теплопроводности Фурье, объясните, как влияет на скорость изменения температур в теле увеличение коэффициента температуропроводности. 40.Какова связь между коэффициентами теплопроводности и температуропроводности и удельной теплоемкостью материалов? Подтвердите эту связь анализом единиц величин.
Вариант 1 (К.р. №1) Задачи Задача 1 (к темам 1 и 2). Считая режим теплопроводности стационарным, определить: а) плотность теплового потока (для плоской формы стенки) или линейную плотность (для цилиндрической формы стенки); б) мощность теплового потока через стенку; в) количество теплоты, прошедшей через стенку за сутки. Изобразить также схематично график распределения температур по толщине стенки. Данные, необходимые для решения своего варианта задачи, выбрать из табл.1.1
Таблица 1.1
Методические указания. При выполнении задачи обратить внимание на правильное использование обозначения тепловых величин и их единиц: q — плотность теплового потока в ваттах на квадратный метр (Вт/м2); ql —линейная плотность теплового потока в ваттах на метр (Вт/м); Q — мощность теплового потока в ваттах (Вт); Q τ —количество теплоты в джоулях (Дж). В качестве образца графического представления температурного поля могут служить рис.2—1, 2—6 [1]. В случае затруднений с решением задачи 1 рекомендуется проанализировать предлагаемое решение обратной задачи: Пусть за сутки стенка в стационарном тепловом режиме пропускает Q τ= 100 МДж теплоты. Температура одной из поверхностей стенки 100°С, противоположной поверхности —90°С. Стенка выполнена из материала с коэффициентом теплопроводности λ=0,1 Вт/(м К). Определить толщину стенки в двух случаях: а) если стенка плоская и имеет площадь поверхности F = 90 м2; б) если стенка цилиндрическая и имеет внутренний диаметр d= 1м и длину 100 м. Определить также для каждого случая мощность теплового потока и удельные значения теплового потока. Дано: Q τ =100 МДж=100
Случай а) стенка плоская, F=90 м2. Случай б): стенка цилиндрическая, длина L=100 м, внутренний диаметр d= 1м. Определить для случаев а) и б) δ, Q,q или Решение. Случай а). Для плоской стенки в стационарном тепловом режиме общее количество теплогы через стенку
Откуда искомая толщина стенки
Искомая мощность теплового потока:
Искомое удельное значение теплового потока (в случае плоской стенки им является плотность теплового потока)
Случай б) Для цилиндрической стенки
Имея в виду,что наружный диаметр цилиндрической стенки D=d+2
Остается подставить в формулу известные значения и решить ее относительно искомой толщины
Откуда искомая толщина цилиндрической стенки
Искомое удельное значение теплового потока (в случае цилиндрической стенки| им является линейная плотность теплового потока)
Ответ:
Задача 2 (к темам 1 и 2). Плоская стальная стенка толщиной Определить коэффициент теплопередачи от газов к воде и удельный тепловой поток через стенку для случаев: а) чистой стенки; б) стенки, покрытой со стороны воды слоем накипи толщиной Значение коэффициента теплопроводности стали принять равным табл. 2.1
Таблица 2.1
Методические указания. При построении графиков распределения в качестве образца может служить рис. 2—3 [1]. В сравнительном анализе графиков следует объяснить повышение температур стальной стенки после образования слоя накипи, а также объяснить различие в наклоне температурного графика, в пределах стальной стенки и в пределах слоя накипи. В случае затруднении с решением задачи 2 рекомендуется проанализировать предлагаемые решения обратной задачи. Пусть стальная стенка толщиной Со стороны воды поверхность стальной стенки покрывается накипью с коэффициентом теплопроводности Дано: Определить: Решение. Один из способов решения этой задачи состоит в следующем. Суммарные термические сопротивления теплопередаче между газом и водой в случае стенки с накипью и без накипи равны
Откуда Следовательно, искомая толщина слоя накипи Таким образом, задача сводится к тому, что сначала надо определить суммарные термические сопротивления после и до образования накипи Вычисляем начальное суммарное термическое сопротивление (до образования накипи)
Конечное суммарное термическое сопротивление вычисляют косвенным путем, используя данные о повышении температуры стенки со стороны газов. Сначала находят начальную плотность теплового потока
Напомним, что при определении разностей температуры 1°С=1 К, именно поэтому здесь Далее, используя формулу Ньютона — Рихмапа,
Согласно условию, температура здесь увеличивается вследствие образования, накипи до значения t”сг=tсг'+ Вновь пользуясь формулой Ньютона—Рихмана, определяют конечную плотность теплового потока между газом и стенкой
Поскольку режим теплопередачи здесь практически стационарен, найденная величина является одновременно плотностью теплового потока между газом и водой (после образования накипи). Это позволяет вычислить конечное суммарное термическое сопротивление.
Теперь можно с помощью выведенной раньше формулы найти искомую толщину слоя накипи
Ответ: повышение температуры стенки на 100°С вызвано образованием трехмиллиметрового слоя накипи.
Задача 3 (к темам 1 и 2). Определить: а) температуру наружной поверхности изоляции; б) суточную потерю теплоты на участке трубы, равном 200 м. Изобразить также схематически график распределения температуры по толщине изоляции и вне ее (в пограничном слое). Данные, необходимые для решения своего варианта задачи, выбрать из табл. 3.1
Таблица 3.1
Методические указания. Перед тем как приступить к решению задач, надо сопоставить расчетные формулы теплопроводности, плоской и цилиндрической стенок. Кроме того, для успешного решения задачи необходимо уяснить связь между суммарным перепадом температур в многослойной стенке и ее суммарным термическим сопротивлением. Суммирование частных термических сопротивлений должно быть осуществлено строго по всем тем и только тем слоям, которые расположены--между изотермическими поверхностями с заданным.значением, температуры. Нельзя допускать, чтобы в расчетную формулу входил перепад температур для одной совокупности слоев, а суммарное термическое сопротивление для другой, хотя бы и в чем-то отличающейся от первой совокупности. В зависимости от условий задачи в совокупность термических сопротивлений следует включать также термическое сопротивление одного или двух пограничных слоев. Эти пограничные слои образуются жидкостями, омывающими стенку. В случае затруднений решением задачи 3 рекомендуется проанализировать предлагаемые решения сходной задачи Определить приближенно: а) температуру наружной поверхности изоляции;б)суточную потерю теплоты на участке трубы, равном 100 м, если наружный диаметр стальной трубы толщина слоя изоляции, покрывающей стенку трубы, Дано: L=100 м; d=0,l м;tст=220°С; О п р е д ел ит ь: Приближенный расчет теплообмена через цилиндрические поверхности часто применяют, если отношение размеров наружного диаметра к внутреннему меньше двух. В пашем случае
Следовательно, приближенный расчет даст хорошее совпадение с точным расчетом Приближенный расчет основан на применении простых формул теплопередачи через плоскую стенку: где В приближенном методе площадь F следует определять через площадь среднего сечения цилиндрической трубы
Заданная разность температур относится к изотермическим поверхностям, между которыми только два слоя: слой изоляции толщиной Поэтому здесь Тогда
Расчет наружной температуры проще всего выполнить, определив сначала плотность теплового потока
Теперь можем определить температуру наружной поверхности изоляции двумя способами: а) используя формулу плоской стенки
б) используя формулу Ньютона-Рихмана q=
О т в е т: Q=0,36 ГДж, Если
Отсюда температура на наружной поверхности изоляции трубы будет:
Задача 4 (к теме 3) Определить температуру в центре и на поверхности пластины толщиной Данные, необходимые для решения своего варианта задачи, выбрать, табл. 4.1
Таблица 4.1
Методические указания. Наиболее удобный путь решения задачи состоит использовании известной теоретической зависимости между относительной безразмерной температурой и критериями Био и Фурье: (t*—tж)/(t0—tж)=f(Fo, Bi). Эта зависимость представлена графиками на рис. 3—4, 3—5 [1] для двух случаев: когда t* есть температура центра (среднего сечения) пластины и когда t* есть температура поверхности пластины. По графикам определяют безразмерную температуру, вычислив сначала значения безразмерных чисел: Fo = Коэффициент температуропроводности а вычисляют по известным значениям плотности, теплоемкости и коэффициента теплопроводности пластины. При вычислении критериев следует помнить, что они безразмерны и что Найдя по графику или.таблице безразмерную относительную температуру, например, для центра пластины, затем, находят по ней и температуру центра пластины, поскольку значения температуры среды tж и начальной температура пластины t0 известны. В случае затруднений с решением задачи 4 рекомендуется проанализировать предлагаемые решения аналогичной задачи, но с нагреванием круглого стержня, бесконечной длины. Круглый стержень диаметром 0,02 м имеет длину во много раз больше диаметра (цилиндр бесконечной длины). Стержень выполнен из пластика с коэффициентом теплопроводности 1 Дано: R= D/2=0,01 м; Определить: Решение: Искомые температуры находятся из соответствующих безразмерных температур, определяемых, в свою очередь, по формулам или графикам через критерии Фурье Fо и Био Bi Вычислим эти критерии для цилиндрического тела: Fo
Безразмерные температуры найдем с помощью графически представленных зависимостей. По графику рис. 3-11 [1] безразмерная температура на оси стержня,при данных значениях F0 и Bi, По графику рис.3-12 [1] безразмерная температура на поверхности стержня при тех же значениях, Пользуясь выражением для безразмерной температуры,
Как и следовало ожидать, при нагревании стержня температура на его поверхности выше, чем на оси Ответ: на оси стержня Вариант 2 (К.р. №1) Задачи Задача1 (к темам 1 и 2). По стальному неизолированному трубопроводу с внутренним диаметром dc1 инаружным dc2 подается пар с температурой t Ж1. Температура окружающей трубопровод среды t Ж2 = 20 °С. Коэффициент теплоотдачи от пара к внутренней поверхности стенки трубы принять постоянным по длине трубопровода и равным Определить потери теплоты с каждого погонного метра трубопровода, температуру наружной t c2 и внутренней tc1 поверхностей трубопровода. Представить график распределения температуры по толщине стенки и в прилегающих к ней пограничных слоях со стороны внутренней и наружной сред, приняв масштабы: по оси температур - 1 см = 50 °С, по радиусу - 1 см = 50 мм. Исходные данные к задаче в табл. 1.2.
Таблица 1.2.
Методические указания. Потери теплоты с одного погонного метра трубопровода равны линейной плотности теплового потока (см. формулу (2.49) в учебнике [1]), а определяемые температуры находятся по формулам (2,48) или (2,48 1) учебника [1], соответствующим граничным условиям третьего рода. Коэффициент теплоотдачи в окружающую среду от наружной стенки трубопровода Задача 2 (к темам 1 и 2). Стальной трубопровод, заданный в задаче 1, покрывают тепловой изоляцией с коэффициентом теплопровод
|

 . Объясните различие в полях температуры каждого слоя.
. Объясните различие в полях температуры каждого слоя. . Объясните различие в полях температуры каждого слоя.
. Объясните различие в полях температуры каждого слоя.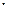 106Дж=100
106Дж=100  =100
=100  С;
С;  =90
=90  .
.





 , из предыдущего уравнения находим
, из предыдущего уравнения находим

 ;
;


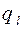 Вт/м
Вт/м
 омывается с одной стороны горячими газами с температурой t1 а с другой — водой с температурой t2.
омывается с одной стороны горячими газами с температурой t1 а с другой — водой с температурой t2. Найти также температуру поверхности стальной стенки со стороны газов в обоих случаях передачи теплоты; построить графики распределения температур по толщине стенки и накипи, указав температуру газов воды, и дать сравнительный анализ этих графиков.
Найти также температуру поверхности стальной стенки со стороны газов в обоих случаях передачи теплоты; построить графики распределения температур по толщине стенки и накипи, указав температуру газов воды, и дать сравнительный анализ этих графиков.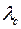 =40
=40  =1,0
=1,0 





 =0,004 м с коэффициентом теплопроводности
=0,004 м с коэффициентом теплопроводности  г=50 Вт/(м2К), от стенки к воде
г=50 Вт/(м2К), от стенки к воде  =5 кВт/(м2К).
=5 кВт/(м2К). с=20 Вт/(мК);
с=20 Вт/(мК);  =920°C; tв=104°C;
=920°C; tв=104°C;  =50 Вт/(м2К);
=50 Вт/(м2К); 



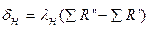


 .определяют начальную (до образования накипи) температуру стальной стенки со стороны газов:
.определяют начальную (до образования накипи) температуру стальной стенки со стороны газов:
 tсг=120°C+100°С=220°С.
tсг=120°C+100°С=220°С.



 , температура на ее поверхности
, температура на ее поверхности 
 , температура окружающего воздуха
, температура окружающего воздуха  =20
=20 
 ;
; 



 — суммарное термическое сопротивление плоских стенок и пограничных слоев.
— суммарное термическое сопротивление плоских стенок и пограничных слоев.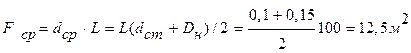


 в среднем сечении стенки (при точном расчете определяют линейную плотность
в среднем сечении стенки (при точном расчете определяют линейную плотность  :
:
 и исходя из температуры стальной стенки
и исходя из температуры стальной стенки  под слоем изоляции и термического сопротивления слоя изоляции:
под слоем изоляции и термического сопротивления слоя изоляции: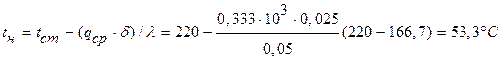
 (Внимание! Для случаев линейной плотности
(Внимание! Для случаев линейной плотности  формула Ньютона-Рихмана принимает вид
формула Ньютона-Рихмана принимает вид  )
) Оба способа привели к одинаковому результату:
Оба способа привели к одинаковому результату:
 ,то приближенный расчет цилиндрической стенки по формулам для плоскости дает значительную ошибку. Поэтому если
,то приближенный расчет цилиндрической стенки по формулам для плоскости дает значительную ошибку. Поэтому если  можно если приравнять линейные плотности теплового потока на поверхности изоляции рассчитанные по закону теплопроводности Фурье и по закону теплоотдачи Ньютона-Рихмана
можно если приравнять линейные плотности теплового потока на поверхности изоляции рассчитанные по закону теплопроводности Фурье и по закону теплоотдачи Ньютона-Рихмана

 через время
через время  после ее погружения в горячую среду (масло или газ), если толщина пластины во много раз меньше ее ширины и длины
после ее погружения в горячую среду (масло или газ), если толщина пластины во много раз меньше ее ширины и длины
 ,Вт/(м К)
,Вт/(м К)



 , Bi =
, Bi =  .
. , удельной теплоемкостью 910 Дж/(кг м) и-плотностью 1100 кг/м3. Исходная температура стержня одинакова по всему его объему и равна 10°С. Определить.температуру на оси стержня и на его поверхности через 100 с после погружения его в горячую среду — газ с температурой 110°С при коэффициенте теплоотдачи 30
, удельной теплоемкостью 910 Дж/(кг м) и-плотностью 1100 кг/м3. Исходная температура стержня одинакова по всему его объему и равна 10°С. Определить.температуру на оси стержня и на его поверхности через 100 с после погружения его в горячую среду — газ с температурой 110°С при коэффициенте теплоотдачи 30 
 К):
К): 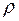 =1100 кг/м3;
=1100 кг/м3;  =30
=30  и:
и:  при
при  , где коэффициент температуропроводности
, где коэффициент температуропроводности

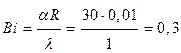


 и решая его относительно t, находим искомые температуры:
и решая его относительно t, находим искомые температуры:

 , на поверхности стержня
, на поверхности стержня 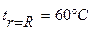
 , коэффициент теплопроводности стальной стенки
, коэффициент теплопроводности стальной стенки  =43
=43  , а коэффициент теплоотдачи от наружной поверхности трубопровода к окружающей среде принять как сумму двух составляющих — конвективной
, а коэффициент теплоотдачи от наружной поверхности трубопровода к окружающей среде принять как сумму двух составляющих — конвективной  и радиационной (излучательной)
и радиационной (излучательной)  .
. :
от пара к стенке
:
от пара к стенке  от стенки к окружающей среде
конвективная составляющая
от стенки к окружающей среде
конвективная составляющая  радиационная составляющая
радиационная составляющая 
 График распределения температуры схематично представлен на рис. 2.7 в учебнике [1]. Подобный же вариант рассмотрен в задаче 1.34 учебного пособия [2].
График распределения температуры схематично представлен на рис. 2.7 в учебнике [1]. Подобный же вариант рассмотрен в задаче 1.34 учебного пособия [2].


