Решение. 1.Среднюю скорость жидкости определяют согласно условию неразрывности струи
1.Среднюю скорость жидкости определяют согласно условию неразрывности струи
Где
F-площадь поперечного сечения струи
Средняя температура жидкости при Средняя температура пограничного слоя при
В качестве
а при Средняя (логарифмическая) разность температур при tc=const
Тогда средняя температура жидкости согласно приведенным выше формулам Соответствующие значения числа Прандтля при вычисленных температурах и температуре стенки можно найти в табл. 5 учебника [1]. интерполируя значения в правой колонке таблицы: Ргж=2,9; Prm=3,4; Ргc =4,31. 3. Согласно формуле (7-35) учебника [1] число Стантона
Мощность теплового потока Qc вычисляют из уравнения теплового баланса жидкости Q=G(h1—h2)=0,0103 (355—209,3) =1,5 кВт, где энтальпии воды на входе и на выходе определяются по четвертой колонке в табл. 5 [1]. Средняя по трубке плотность теплового потока
где площадь поверхности трубки F=
Чтобы вычислить теперь St, надо кроме уже найденных Согласно условию задачи в качестве определяющей следует принять среднюю температуру воды, Согласно табл. 5 [1], при этой температуре
Ответ:
Задача 2 (к темам 4—8). Определить мощность теплового потока, характеризующего конвективную теплоотдачу в струе жидкости, протекающей по трубе заданного диаметра длиной 3 м. Обосновать выбор расчетного уравнения, применяемого при решении задачи. Данные, необходимые для решения этой задачи, выбрать из табл. 6.1
Таблица 6.1
Методические указания. Мощность теплового потока (в Вт) определяется по формуле Ньютона — Рихмана: Поэтому необходимо вычислить площадь поверхности стенки трубы, средний коэффициент теплоотдачи При выборе расчетного безразмерного уравнения следует учесть значение числа Рейнольдса. Особое внимание при действиях с расчетным уравнением нужно уделять определяющей температуре, указываемой с помощью индексов при числах подобия. В соответствии с полученным числовым значением определяющей температуры выписывают из таблицы теплофизических свойств, приведенной, например, в приложении к учебнику, нужные значения этих свойств и с их помощью вычисляют сначала значение определяющих чисел подобия, входящих в безразмерное уравнение, а затем с помощью этого уравнения и значение среднего числа Нуссельта. По значению среднего числа Нуссельта находят средний коэффициент теплоотдачи где В случае затруднения с решением задачи 2 рекомендуется проанализировать решение аналогичной задачи. Дано: длина трубы l=1м: внутренний диаметр трубы d= 0,1 м; температура стенки трубы tс=100°С; средняя логарифмическая температура жидкости tж=60 Определить мощность теплового потока через стенку трубы Qc. Решение. Искомую мощность определяют по формуле Ньютона — Рихмана Qc= Средний коэффициент теплоотдачи
где кинематический коэффициент вязкости Оба значения числа Прандтля>1. Г—относительная длина трубы: Для найденных характеристик рекомендуется в [1] безразмерное уравнение (8-11) с поправочным множителем Где Подставляя в это уравнение полученные выше числовые значения,находим
По значению
где коэффициент теплопроводности находится по табл.7 [1] при Кроме Площадь поверхности трубки, омываемой маслом, Средний логарифмический температурный напор между стенкой и жидкостью по длине трубки Тогда согласно приведенной выше формуле искомая мощность теплового потока через стенку трубы Qc=0,314 Ответ: мощность теплового потока через стенку трубы Задача 3 (к темам 4—2). Определить мощность тепловою потока, характеризующую конвективную теплоотдачу от поверхности объекта — трубы заданного диаметра длиной 40 м или вертикальной стенки заданной высоты при ширине 15 м. Обосновать выбор критериальной формулы, примененной для peшения. задачи. Данные, необходимые для решения своего варианта задачи, выбрать из табл. 7.1
Таблица 7.1
Методические указания. Следует иметь в виду, что в задаче рассматривается только конвективная составляющая теплоотдачи. Суммарная геплоотдача (с учетом теплового излечения) обычно больше своей конвективной составляющей, но здесь задача по определению суммарной теплоотдачи не ставится. Как и в предыдущей задаче, нужно внимательно следить за правильностью выбора определяющей температуры. При вычислении критерия Грасгофа следует обратить внимание на особенность определения коэффициента объемного расширения
В общем случае значение этого коэффициента зависит от давления и температуры и вычисляется по следующей интерполяционной формуле:
где Для насыщенного водяного пара и для воды на линии насыщения значения коэффициентов объемного расширения приводятся в справочных таблицах рекомендуемой учебной литературы. Вода при давлениях меньше 10 МПа имеет коэффициент объемного расширения, который при данной температуре практически не зависит от давления и поэтому его можно определять по табличным значениям, приведенным для данной температуры на линии насыщения воды. Наконец газы, а также воздух, который можно рассматривать как идеальные, характеризуюся коэффициентом объемного расширения, который определяется с помощью уравнения Клапейрона —.Менделеева (он равен величине, обратной абсолютной температуре
Вариант 2 (К.р. №2) Задачи
Задача 1 (к темам 4-8). По трубке с внутренним диаметром d = 16 мм длиной l = 2,1 м течет (горячее) жидкое масло, отдающее теплоту через стенку трубы, охлаждаемую извне. Расход масла по трубке G= 0,0091 кг/с; температура масла на входе tж.1 = 90 ° С, на выходе tж.2 = 30 ° С; температуру стенки принять постоянной по длине трубки и равной заданному значению tc. Вычислить заданные числа подобия, приняв в качестве определяющей температуры заданное ее значение, в качестве определяющего размера принять внутренний диаметр трубки, в качестве расчетного температурного напора - среднюю (логарифмическую) разность температур между жидкостью и стенкой. Представить график изменения температур жидкости и стенки по длине трубки, указать на графике заданные значения определяющей температуры и расчетного температурного напора. Данные, необходимые для выбора своего варианта условиям задачи, приведены в табл. 5.2. Таблица 5.2.
Методические указания даны в первом варианте. Физические свойства масел приведены в приложении 3. Задача 2 (к темам 4-8). Определить мощность теплового потока, характеризующего конвективную теплоотдачу к струе жидкости, протекающей по трубе заданного диаметра длиной 3 м. Обосновать выбор расчетного уравнения, применяемого при решении задачи. Данные, необходимые для решения этой задачи, выбрать из табл.6.2.
Методические указания даны в первом варианте. Задача 37 (к темам 4-9). Определить мощность теплового потока, характеризующую конвективную теплоотдачу от поверхности объекта - трубы заданного диаметра длиной 4,0 м или вертикальной стенки заданной высоты при ширине 10 м. Обосновать выбор безразмерного уравнения, примененного для решения задачи. Данные, необходимые для решения своего варианта задачи, выбрать из табл.7.2. Методические указания даны в первом варианте. Таблица 7.2.
Вариант 3 (К.р.№ 2)
|

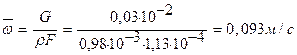
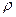 —средняя плотность воды в заданном интервале температур 50—80°С и согласно табл. 5 учебника [1],
—средняя плотность воды в заданном интервале температур 50—80°С и согласно табл. 5 учебника [1],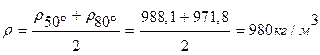

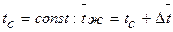 ;
;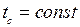
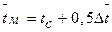
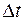 выбираем среднюю логарифмическую разность температур, потому что отношение температурных напоров на входе в трубку и выходе
выбираем среднюю логарифмическую разность температур, потому что отношение температурных напоров на входе в трубку и выходе
 >2 средняя арифметическая разность температур дает слишком приближенные значения.
>2 средняя арифметическая разность температур дает слишком приближенные значения.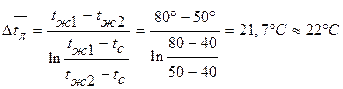
 =40°+22°=62°С, а средняя температура пограничного слоя
=40°+22°=62°С, а средняя температура пограничного слоя 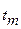 =40+0,5
=40+0,5  22°=51°С.
22°=51°С. . Г де плотность р и теплоемкость Ср предстоит найти с помощью таблицы физических свойств воды по определяющей температуре, а средний коэффициент теплоотдачи
. Г де плотность р и теплоемкость Ср предстоит найти с помощью таблицы физических свойств воды по определяющей температуре, а средний коэффициент теплоотдачи  — из формулы Ньютона — Рихмана:
— из формулы Ньютона — Рихмана:
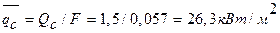 ,
,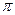
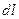 =3,14• 0,012 1,5 м = 0,057. Тогда средний коэффициент теплоотдачи
=3,14• 0,012 1,5 м = 0,057. Тогда средний коэффициент теплоотдачи
 и
и 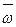 найти также
найти также 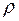 и Cp при заданной определяющей температуре.
и Cp при заданной определяющей температуре.
 К). Тогда искомая величина
К). Тогда искомая величина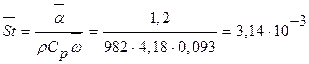


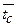

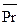

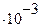

 . Величину
. Величину  находят из безразмерного уравнения, которое предстоит выбрать.
находят из безразмерного уравнения, которое предстоит выбрать.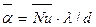 ,
,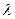 — значение коэффициента теплопроводности, полученное из таблиц в соответствии с уже известной определяющей температурой. Средний температурный напор
— значение коэффициента теплопроводности, полученное из таблиц в соответствии с уже известной определяющей температурой. Средний температурный напор 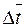 находят согласно указаниям, данным в пояснениях к расчетному безразмерному уравнению.
находят согласно указаниям, данным в пояснениях к расчетному безразмерному уравнению. С; род жидкости — трансформаторное масло; средняя скорость течения жидкости по трубе
С; род жидкости — трансформаторное масло; средняя скорость течения жидкости по трубе 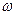 =10 м/с.
=10 м/с.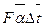
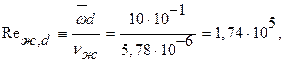
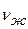 находят по заданной средней температуре масла tж=60°С в табл.7. учебника [1]. Полученное значение
находят по заданной средней температуре масла tж=60°С в табл.7. учебника [1]. Полученное значение 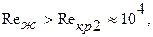 следовательно заданный режим течения является развитым турбулентным. В – соотношение тодщин гидродинамического и теплового пограничных слоев; определяется по числу Прандтля при температурных
следовательно заданный режим течения является развитым турбулентным. В – соотношение тодщин гидродинамического и теплового пограничных слоев; определяется по числу Прандтля при температурных  ;
; 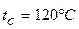 ; Prж =87,8; Prc=34,9 (находятся по табл.7 Учебника [1].
; Prж =87,8; Prc=34,9 (находятся по табл.7 Учебника [1].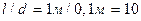
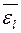 (8-14):
(8-14): 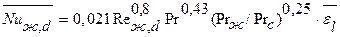

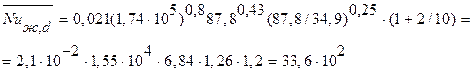
 вычисляем
вычисляем
 .
. t.
t.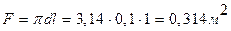
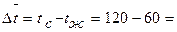 60°С
60°С .
.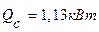
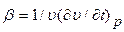
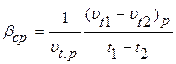
 удельные объемы, определяемые по таблицам для данного вещества в окрестностях заданного состояния жидкости (пара, газа) с удельным объемом
удельные объемы, определяемые по таблицам для данного вещества в окрестностях заданного состояния жидкости (пара, газа) с удельным объемом 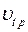 . Окрестные состояния 1 и 2 должны быть выбраны так, чтобы их давления были одинаковыми с заданным давлением (Р1=P=Р2), а темперятуры отличались, (t1>t>t2). В частности так определяют коэффициент объемного расширения перегретого пара. В качестве t здесь должна быть использована определяющая температура
. Окрестные состояния 1 и 2 должны быть выбраны так, чтобы их давления были одинаковыми с заданным давлением (Р1=P=Р2), а темперятуры отличались, (t1>t>t2). В частности так определяют коэффициент объемного расширения перегретого пара. В качестве t здесь должна быть использована определяющая температура )
)


