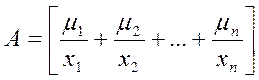Определения четких и нечетких множеств. Определение нечеткого множества. Функция принадлежности. Примеры нечетких дискретных и непрерывных множеств.
Нечеткая логика. Краткие исторические сведения. Аспекты неполноты информации 1965г. – Л. Заде опубликовал свою первую работу по нечеткой логике. Она положила начало новому направлению. 1987г. – управление метро около Токио. Этому предшествовал принцип, который высказал Неймон (основоположник кибернетики): «Стремление получить точную, исчерпывающую модель для сложной системы не имеет смысла, т.к. сложность модели становится соизмеримой со сложностью системы. Чем сложнее система, тем менее мы способны дать точные и имеющие практический смысл суждений о ней». Л.Заде: «для систем, сложность которых превосходит некоторый пороговый уровень, точность и фактический смысл (точный, полный анализ) не имеет практического значения. Аспекты неполноты информации: 1) Неточность 2) Неопределенность 3) Нечеткость 4) Случайность Нечеткость – множества, которые имеют размытые границы, (элементы относятся к тому или иному множеству с определенной степенью уверенности (принадлежности)). Определения четких и нечетких множеств. Определение нечеткого множества. Функция принадлежности. Примеры нечетких дискретных и непрерывных множеств. Нечеткость – понятие, относящееся к таким множествам, в которых возможны градация степени принадлежности к ним, от полной принадлежности до полной не принадлежности, т.е. такой класс объектов в котором нет резкой границы между объектами с полной принадлежностью к нему и его окружением. Четкое множество – множество, которое задано в виде множества пар
Нечеткое множество считается заданным, если задано множество пар В нечетком множестве вводится понятие функции принадлежности
Существует также нечеткие дискретные множества, которые формируются при известной функции
|

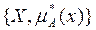 , где X€AcX,
, где X€AcX, 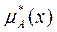 - функция принадлежности
- функция принадлежности


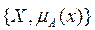

 , которая показывает степень принадлежности элемента X множеству A.
, которая показывает степень принадлежности элемента X множеству A.