Ступенчатый профиль показателя преломления
Стандартная процедура разделения переменных состоит в представлении возможных решений, например, для Ez компонент, в виде:
где A – постоянный множитель. Так же как и в случае прямоугольных волноводов предположим, что зависимость от координаты z имеет вид
где β; – постоянная распространения световой волны вдоль направления оптической оси. Также, вследствие симметрии конструкции волновода, каждая компонента поля не должна меняться при изменении угла φ; на 2 π;, поэтому
В уравнении (79), постоянная величина ν; может принимать только целочисленные значения: ν=0, ±1, ±2, …, т.к. поле должно быть периодическим при изменении φ; с периодом 2 π;. Подставляя (79) и (80) в (77), получаем:
Это хорошо известное выражение, решениями которого являются функции Бесселя. Точно такое же уравнение имеет место и для Hz. Рассмотрим однородный сердечник волокна с показателем преломления равным n 1 с радиусом a, окруженным оболочкой с радиусом, существенно превышающим размер сердечника с показателем преломления n 2. В этом случае характер распространения световых волн не зависит от радиуса оболочки по причине быстрого затухания световых волн в этой среде. Кроме того, реальные световые волокна имеют радиус оболочки значительно больший, чем радиус сердцевины. Вначале надо определить, какие из функций Бесселя являются подходящими в этом случае. Если q – действительное число, то решениями уравнения (81) являются либо
Число ν;, которое может принимать только целочисленные значения, называется порядком функции, а qr – аргументом функции. Графики функций Jν (qr) и Yν (qr) для нескольких первых значений ν; приведены на рис.18, 19.
рис.18. График функций Бесселя первого рода для действительного значения q при значениях ν;=0, 1, 2.
рис.19. График функций Бесселя второго рода для действительного значения q при значениях ν;=0, 1, 2. Можно видеть, что за исключением J 0 все остальные функции Бесселя первого рода стремятся к нулю при стремлении к нулю аргумента функций. При этом только J 0 стремиться к единичному значению. С другой стороны, функции Бесселя Yν расходятся при стремлении аргумента к нулю, поэтому они должны быть исключены из решения задачи. Функции первого рода монотонно уменьшаются при стремлении аргумента к бесконечности, поэтому правильная комбинация этих функций является решением для распределения светового поля внутри сердечника оптоволокна. Решениями уравнения Бесселя, которые появляются при решении внешней краевой задачи (оболочка оптоволокна)
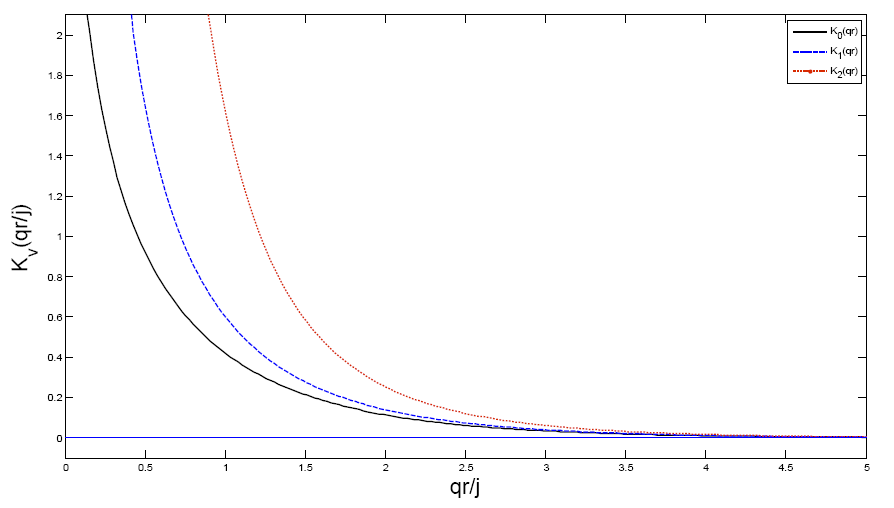
являются модифицированные функции Бесселя Iν (qr) и Kν (qr) первого и второго рода. Графики этих функций показаны на рис.20, 21.
рис.20. Модифицированные функции Бесселя первого рода Iν (qr) для действительного значения q при значениях ν;=0, 1, 2.
рис.21. Модифицированные функции Бесселя второго рода Kν (qr) для действительного значения q при значениях ν;=0, 1, 2. Из рассмотрения графиков 20 и 21 следует, что Iν (qr) неограниченно возрастает при стремлении аргумента к бесконечности. С другой стороны, функция Kν (qr) быстро стремится к нулю при увеличении аргумента. Т.к. мы ищем ограниченное решение внешней краевой задачи для оболочки, то единственными подходящими функциями в этом случае являются модифицированные функции Бесселя второго рода Kν (qr). Т.о., для r < a решениями задачи распространения света по оптоволокну являются функции Бесселя первого рода Jν (ur) порядка ν;. При этом u 2= k 12- β;2, где k 1=2π n 1/ λ;, λ; – длина световой волны в вакууме. Выражения для Ez и Hz внутри сердцевины волновода (r<a) имеет вид:
Вне сердцевины, т.е. в области оболочки решениями будут модифицированные функции Бесселя второго рода, Kν (wa), где w 2= β;2- k 22, k 2=2π n 2/ λ;:
где A, B, C, D – произвольные постоянные, определяющиеся из граничных условий. Для световых мод, распространяющихся по оптоволокну, константы распространения мод удовлетворяют условию β;2< β;< β;1 вне и внутри сердцевины волокна. Если n 2 k ≤ β;≤ n 1 k, то распространение светового поля внутри сердцевины имеет осциллирующий характер и энергия поля быстро уменьшается по мере проникновения в оболочку волокна. В этом случае световая энергия поля сосредоточена в основном в сердцевине и распространяется без потерь вдоль оптоволокна.
|

 , (78)
, (78) , (79)
, (79) . (80)
. (80) . (81)
. (81) - функция Бесселя первого рода, или
- функция Бесселя первого рода, или - функция Бесселя второго рода.
- функция Бесселя второго рода.

 , (82)
, (82)
 (83)
(83) . (84)
. (84)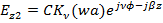 (85)
(85) , (86)
, (86)


