Граничные условия
Граничными условиями для TE компонент поля является равенство тангенциальных компонент Eφ и Ez при r = a. Точно такое же равенство должно иметь место для тангенциальных компонент магнитного поля Hφ и Hz при r = a,
Эти граничные условия дают четыре уравнения для произвольных постоянных A, B, C и D. При этом q 2= u 2= k 12- β;2, где k 1=2π n 1/ λ;, λ; – длина световой волны в вакууме, в то время как для оболочки q 2= w 2= β;2- k 22, где k 2=2π n 2/ λ;. Используя (88), имеем:
Используя (87) и (73) совместно с (83) и (84), получаем:
где верхние черточки означают дифференцирование по u и w аргументу. Точно также, относительно тангенциальных компонент магнитного поля при r = a, имеем:
и
Выражения (91)-(94) представляют систему четырех уравнений с четырьмя неизвестными (коэффициенты) без правой части. Ненулевые решения этой системы можно найти из условия равенства нулю определителя этой системы:
где
Вычисление определителя (95) позволяет определить показатели распространения β;, соответствующие разрешенным модам распространения из следующего нелинейного уравнения:
Выражение (97) называется характеристическим уравнением рассматриваемой краевой задачи распространения света в оптоволокне. Константа β определяется численными методами при условиях u 2= k 12- β;2 и w 2= β;2- k 22.
|

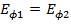 (87)
(87) 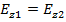 (88)
(88) 
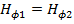 (89)
(89) 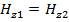 . (90)
. (90) . (91)
. (91)
 , (92)
, (92) (93)
(93)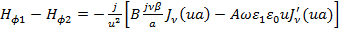
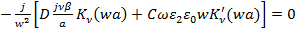 . (94)
. (94) , (95)
, (95)


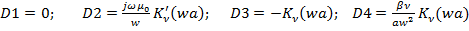 . (96)
. (96)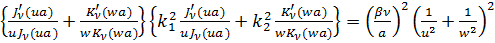 . (97)
. (97)


