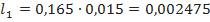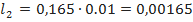Расчет согласующей цепи
Расчетная графическая работа По дисциплине «Устройства СВЧ и Антенны»
Выполнил: студент группы РТЭ 41-10 Владимирова А.А. Проверил: Иванов В.Н
Чебоксары 2013 Содержание
Проектирование полосовых фильтров на элементах с распределенными параметрами Проектирование кольцевого моста Расчет ступенчатых трансформаторов Расчет согласующей цепи
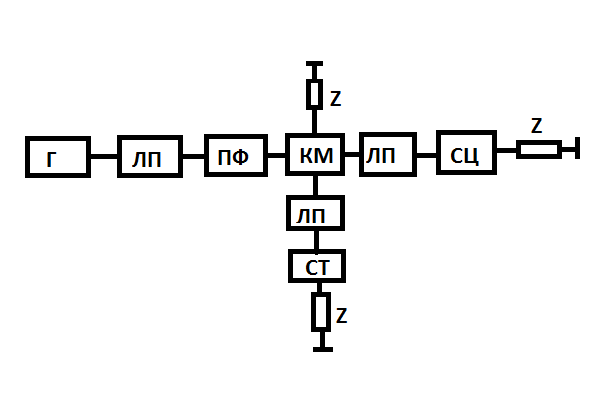
Г- генератор, ЛП- линии передачи ,ПФ- полосовой фильтр, КМ- кольцевой мост, СЦ- согласующая цепь, СТ- ступенчатый трансформатор.
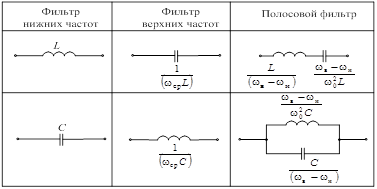
1.Проектирование полосовых фильтров на элементах с распределенными параметрами Таблица 3.2 Преобразования элементов фильтров
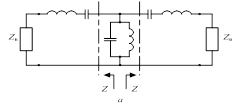
Рис. 3.16. Процедура реализации полосового фильтра (начало): а – эквивалентная схема трехзвенного полосового фильтра
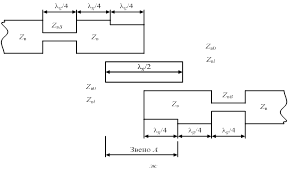
Рис. 3.16.г) Процедура реализации полосового фильтра реализация фильтра с помощью параллельных шлейфов
Рис. 3.16. Процедура реализации полосового фильтра (продолжение): ж – конструкция фильтра на встречных стержнях с модифицированными концевыми отрезками Задание:Сконструировать полосовые фильтры на основе топологий. Конструируемые фильтры должны иметь Чебышевскую характеристику с амплитудой осцилляции в полосе пропускания 1 дБ, и их следует синтезировать на основе трехзвенного фильтра-прототипа нижних частот из сосредоточенных элементов. Ширина полосы пропускания фильтров 30 МГц при центральной частоте 2 ГГц. Фильтры должны быть в микрополосковом исполнении и сопрягаться с 50-омной линией. Решение Дано: f 0 = 2 ГГц; f в – f н = 30 МГц; Z в= Z н= 50 Ом; n = 3; амплитуда осцилляции 1 дБ. По программе для фильтра с чебышевской характеристикой находим: g -параметры определяются по следующим формулам: ωcp = 1, g 0 = gn +1 =1,
где аргумент синуса выражен в радианах.
g 0 = g 4 = 1; g 1 = g 3 = 1,0315; g 2 = 1,1474. Воспользуемся преобразованием, трансформирующим фильтр нижних частот в полосовой, что приводит к схеме рис. 3.16, а, и определим L н и С н:
Находим истинные значения L н и С н при заданном сопротивлении нагрузки:
L н = 821 нГн; С н = 328 пФ. Синтезируем фильтр, опираясь на топологию (см. рис. 3.16, г). Пусть Z в1 = 25 Ом; Zв2 = 100 Ом. Преобразования элементов фильтров
Здесь Z в – сопротивление, с которым сопрягается фильтр. Параметры g 1и g 2определяются при расчете нормированного фильтра-прототипа нижних частот; В – относительная полоса пропускания фильтра; В= (ωв – ωн)/ω0. Тогда B =(ωв –ωн) /ω0=30
На основании данных табл. 3.3 L 1= Z в1 C н f λ g 1 =25·328·10-12 ·2·109 λ g 1=16,4 λ g 1, L 2= Z н f λ g 2 / Z в2 = (821·10-9 ·4·109 λ g 1 )/100=32,84 λ g 1. Синтезируем фильтр, опираясь на топологию рис. 3.16, ж. В этой конструкции Z в B эквивалентно Z в А в уже рассмотренной конструкции, т. е. Z в B = 216 Ом; Z в = 50 Ом. Выберем K в (3.22) и (3.23) равным Z в А для рассмотренной конструкции, тогда:
Наконец, рассмотрим третью реализацию фильтра, соответствующую рис. 3.16, з. Как и в предыдущей конструкции, Z в. еА = 64,16 Oм; Z в0 А = 35,85 Ом. Теперь с помощью (3.22) и (3.23) при K = 104 Ом вычислим:
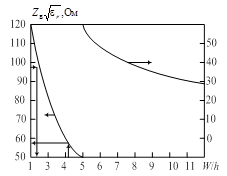
По найденным значениям находим ширину полосок, расстояние между ними и длины волн в дополнительных отрезках связанных линий. На этом проектирование заканчивается. Из рис.3.16 г) находим Рис. 1.2. Зависимость волнового сопротивления от W / h для микрополосковой линии с полоской бесконечно малой толщины
То по графику получим: Для
|

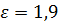
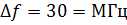

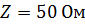

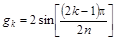 , k =1,2,3,… n,
, k =1,2,3,… n,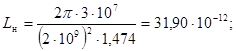
 .
. ;
; 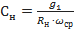 ; ωср = = 2p×107 рад/с и R н = 50 Ом:
; ωср = = 2p×107 рад/с и R н = 50 Ом: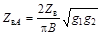 ;
;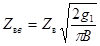 .
.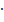 2π·107/2
2π·107/2 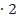 π·109 =
π·109 = 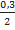 ; l =
; l = 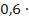 λ gA /4; Z в А =
λ gA /4; Z в А =  =216;
=216;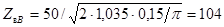 .
.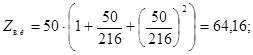
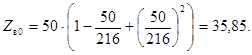
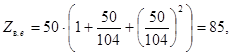
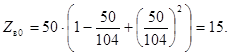
 и
и 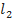 для фильтра с параллельными шлейфами:
для фильтра с параллельными шлейфами: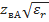 =295,9Ом
=295,9Ом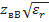 =142,5 Ом
=142,5 Ом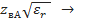 W / h=
W / h=  , а
, а 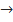 W / h=
W / h= 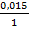 ;
;