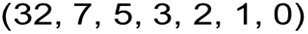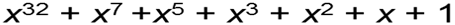| N теста
| Значение
| Гипотеза
| Вывод
|
|
| n0=10162 n1=9838
| (9654; 10346) (9654; 10346)
| + +
|
|
| 
| (1.03, 57,4)
| +
|
|
| F3(2)=2438 F3(3)=1301 F3(4)= 626 F3(5)=336 F3(6)=142 F3(7+)=157
| (2267, 2733) (1079, 1421) (502, 748) (223, 402) (90, 223) (90, 223)
| + + + + + +
|
|
| F4=17
| < 34
| +
|
 Сдвиговые регистры с обратной связью.
Сдвиговые регистры с обратной связью.


Поточные шифры на регистрах сдвига с линейной обратной связью (Linear feedback shift regiser=LFSR)
Есть несколько причин использования линейных регистров сдвига в криптографии:
- высокое быстродействие криптографических алгоритмов
- применение только простейших операций сложения и умножения, аппаратно реализованных практически во всех вычислительных устройствах
- хорошие криптографические свойства (генерируемые последовательности имеют большой период и хорошие статистические свойства)
- легкость анализа с использованием алгебраических методов за счет линейной структуры

Регистр сдвига с линейной обратной связью.
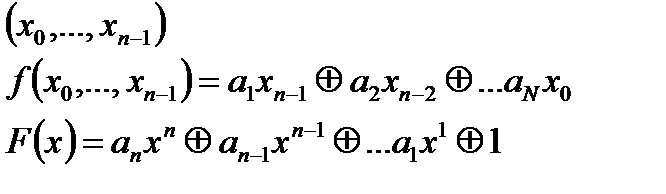

Пример: Возьмём неприводимый примитивный многочлен 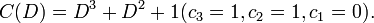 Этот многочлен можно записать, как
Этот многочлен можно записать, как  – выписаны степени, при которых стоят ненулевые коэффициенты.
– выписаны степени, при которых стоят ненулевые коэффициенты.
Запишем в исходном состоянии в ячейки 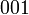 и определим длину периода генератора:
и определим длину периода генератора:
| Таблица. Определение периода генератора
|
| Обратная связь
| Ячейка2
| Ячейка1
| Ячейка0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Период генератора равен  На выходе генератора будет последовательность:
На выходе генератора будет последовательность:
Последовательность удовлетворяет постулатам Голомба.
Пример.
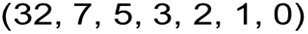


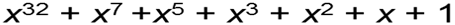
Приведём примеры некоторых примитивных многочленов по модулю 2:



 Сдвиговые регистры с обратной связью.
Сдвиговые регистры с обратной связью.
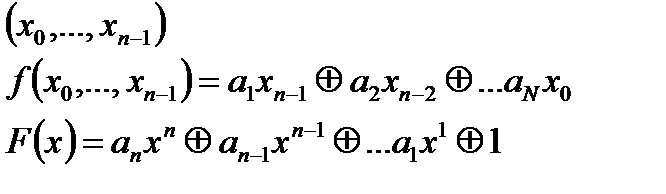

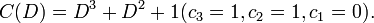 Этот многочлен можно записать, как
Этот многочлен можно записать, как  – выписаны степени, при которых стоят ненулевые коэффициенты.
– выписаны степени, при которых стоят ненулевые коэффициенты.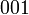 и определим длину периода генератора:
и определим длину периода генератора: На выходе генератора будет последовательность:
На выходе генератора будет последовательность: