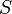- бесконечная последовательность с членами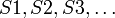 
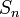– конечная последовательность длины 
.
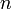Говорят, что РСЛОС генерирует последовательность 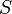, если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает с 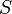. Аналогично, говорят, что РСЛОС генерирует конечную последовательность 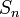, если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых 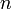членов члены последовательности .
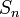Наконец дадим определение линейной сложности бесконечной двоичной последовательности.
Определение: Линейной сложностью бесконечной двоичной последовательности 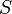называется число 
, которое определяется следующим образом:
- Если 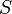– нулевая последовательность
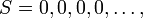, то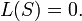 
- Если не существует РСЛОС, который генерирует 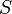, то равно бесконечности.
- Иначе, есть длина самого короткого РСЛОС, который генерирует .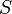
Эффективным алгоритмом определения линейной сложности конечной двоичной последовательности является алгоритм Берлекемпа-Месси.
