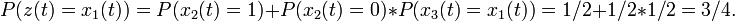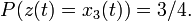


Известно, что каждая Булева функция  может быть записана как сумма по модулю 2 произведений порядков
может быть записана как сумма по модулю 2 произведений порядков 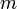 независимых переменных,
независимых переменных,  . Это выражение называется алгебраической нормальной формой функции
. Это выражение называется алгебраической нормальной формой функции 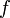 . Нелинейным порядком функции
. Нелинейным порядком функции 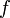 называется максимальный порядок членов в записи её алгебраической нормальной формы.
называется максимальный порядок членов в записи её алгебраической нормальной формы.
Например, Булева функция 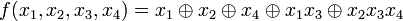 имеет нелинейный порядок 3. Максимально возможный нелинейный порядок Булевой функции равен количеству переменных
имеет нелинейный порядок 3. Максимально возможный нелинейный порядок Булевой функции равен количеству переменных 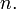
Предположим теперь, что у нас 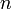 регистров сдвига с линейной обратной связью, их длины
регистров сдвига с линейной обратной связью, их длины  попарно различны и больше двух. Все регистры объединены нелинейной функцией
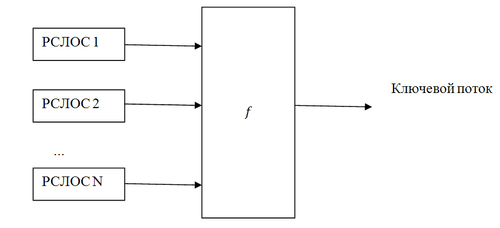
попарно различны и больше двух. Все регистры объединены нелинейной функцией  , как показано на рисунке. Функция
, как показано на рисунке. Функция 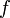 представлена в алгебраической нормальной форме. Тогда линейная сложность потока ключей равна
представлена в алгебраической нормальной форме. Тогда линейная сложность потока ключей равна  .
.
Если 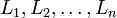 – попарно взаимно-простые числа, то длина периода ключевого потока равна:
– попарно взаимно-простые числа, то длина периода ключевого потока равна: 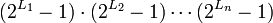 . Например, если
. Например, если  , то
, то 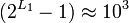 . И длина периода ключевого потока равна
. И длина периода ключевого потока равна 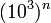 .
.


Генератор Геффа
Пример (генератор Геффа):
В этом генераторе используются три РСЛОС, объединённые нелинейным образом. Длины этих регистров  попарно простые числа.
попарно простые числа.
Нелинейную функцию для данного генератора можно записать следующим образом:

Длина периода: 
Линейная сложность: 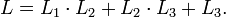
Генератор Геффа криптографически слаб, потому что информация о состояниях генераторов РСЛОС 1 и РСЛОС 3 содержится в его выходной последовательности. Для того чтобы понять это, обозначим 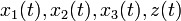
 -ые выходные биты РСЛОС 1,2,3 и потока ключей, соответственно. Тогда корреляционная вероятность последовательности
-ые выходные биты РСЛОС 1,2,3 и потока ключей, соответственно. Тогда корреляционная вероятность последовательности 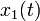 по отношению к последовательности
по отношению к последовательности 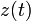 :
:
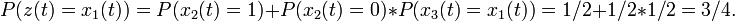
Аналогично, 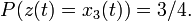
По этой причине, несмотря на длинный период и достаточно высокую линейную сложность, генератор Геффа поддаётся корреляционным атакам.


Генератор на нелинейном фильтре



 может быть записана как сумма по модулю 2 произведений порядков
может быть записана как сумма по модулю 2 произведений порядков 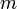 независимых переменных,
независимых переменных,  . Это выражение называется алгебраической нормальной формой функции
. Это выражение называется алгебраической нормальной формой функции 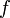 . Нелинейным порядком функции
. Нелинейным порядком функции 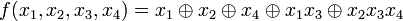 имеет нелинейный порядок 3. Максимально возможный нелинейный порядок Булевой функции равен количеству переменных
имеет нелинейный порядок 3. Максимально возможный нелинейный порядок Булевой функции равен количеству переменных 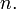
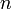 регистров сдвига с линейной обратной связью, их длины
регистров сдвига с линейной обратной связью, их длины  попарно различны и больше двух. Все регистры объединены нелинейной функцией
попарно различны и больше двух. Все регистры объединены нелинейной функцией  , как показано на рисунке. Функция
, как показано на рисунке. Функция  .
.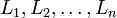 – попарно взаимно-простые числа, то длина периода ключевого потока равна:
– попарно взаимно-простые числа, то длина периода ключевого потока равна: 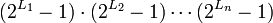 . Например, если
. Например, если  , то
, то 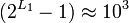 . И длина периода ключевого потока равна
. И длина периода ключевого потока равна 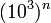 .
.
 попарно простые числа.
попарно простые числа.

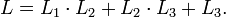
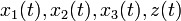
 -ые выходные биты РСЛОС 1,2,3 и потока ключей, соответственно. Тогда корреляционная вероятность последовательности
-ые выходные биты РСЛОС 1,2,3 и потока ключей, соответственно. Тогда корреляционная вероятность последовательности 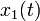 по отношению к последовательности
по отношению к последовательности 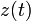 :
: