Неопределенный интеграл. Подробные примеры решений

На данном уроке мы начнем изучение темы Неопределенный интеграл, а также подробно разберем примеры решений простейших (и не совсем) интегралов. Как обычно, я ограничусь минимумом теории, наша задача – научиться решать интегралы.

Что нужно знать для успешного освоения материала? Для того чтобы справиться с интегральным исчислением Вам необходимо уметь находить производные, минимум, на среднем уровне. Не лишним опытом будет, если у Вас за плечами несколько десятков (лучше – сотня) самостоятельно найденных производных. По-крайне мере, Вас не должны ставить в тупик задания на дифференцирование простейших и наиболее распространенных функций. Казалось бы, при чем здесь вообще производные, если речь в статье пойдет об интегралах?! А дело вот в чем. Дело в том, что нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия, как, например, сложение/вычитание или умножение/деление. Таким образом, без навыка (+ какого-никакого опыта) нахождения производных, к сожалению, дальше не продвинуться.

В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов.

В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования. И, если способ интегрирования изначально подобран неверно (т.е. Вы не знаете, как решать), то интеграл можно «колоть» буквально сутками, как самый настоящий ребус, пытаясь приметить различные приемы и ухищрения. Некоторым даже нравится.

Коль скоро способов решения существует очень много, то с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на мой взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах. Потом нужно детально проработать метод замены в неопределенных интегралах. ЭТО ВАЖНЕЙШИЙ ПРИЁМ! И, в-третьих, обязательно следует ознакомиться с методом интегрирования по частям, поскольку с помощью него интегрируется обширный класс функций. Если Вы освоите хотя бы эти три урока, то уже «не два». Вам могут «простить» незнание интегралов от тригонометрических функций, интегралов от дробей, интегралов от дробно-рациональных функций, интегралов от иррациональных функций (корней), но вот если «сесть в лужу» на методе замены или методе интегрирования по частям – то это будет очень и очень скверно.

Знания и навыки по неопределенному интегралу потребуются в дальнейшей учебе, в частности, при изучении определенного интеграла. Необходимость взять интеграл возникает даже в теории вероятностей!

Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:

Сразу разбираемся в обозначениях и терминах:

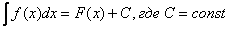
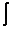– значок интеграла.

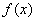– подынтегральная функция (пишется с буквой «ы»).

– значок дифференциала. Что это такое мы рассмотрим совсем скоро. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.

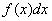– подынтегральное выражение или «начинка» интеграла.

– первообразная функция.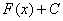

– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа .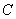