Эргодические цепи
Как указывалось выше под эргодической ДМЦ понимается цепь, не имеющая невозвратных состояний. Таким образом, в такой цепи возможны любые переходы между состояниями. Напомним, что эргодические цепи могут быть регулярными и циклическими. Определение таких цепей было дано выше. Поскольку согласно данному выше определению в эргодической ДМЦ на любом шаге должны быть возможными любые переходы, то очевидно при этом, что переходные вероятности не должны равняться нулю. Оказывается, из этого условия вытекают некоторые замечательные свойства регулярных ДМЦ:
a = < а1, а2... аn >, (8.12) все компоненты которого положительны. Вектор (8.12) в теории ДМЦ занимает особое место из-за наличия многих приложений и называется вектором предельных или финальных вероятностей (иногда - стационарным вектором). Финальные вероятности определяют с помощью векторно-матричного уравнения
которое в развернутом виде будет выглядеть так:
К уравнениям (8.13а) можно дополнительно добавить условие нормировки:
Тогда любое из уравнений в (8.14) можно исключить. Также как и в случае поглощения ДМЦ многие характеристики эргодических цепей определяются с помощью фундаментальной матрицы, которая в этом случае будет иметь вид:
Для эргодических цепей характеристикой, имеющей важное практическое значение, является продолжительность времени, за которое процесс из состояния Si впервые попадает в Sj, так называемое время первого достижения. Матрица средних времен достижения определяется по формуле:
где Mz - фундаментальная матрица (8.15); Mzdg - диагональная матрица, образованная из фундаментальной, заменой всех элементов, кроме диагональных - нулями; D - диагональная матрица с диагональными элементами d ii= 1/a i; Е - матрица, все элементы которой равны единице. Матрица дисперсий времени первого достижения имеет несколько более сложный вид:
где кроме уже упомянутых обозначений встречается новое - (МzЧ Мt) dg, обозначающее диагональную матрицу, полученную из матричного прозведения матриц МzЧ Мt.
|

 , (8.13)
, (8.13) (8.13а)
(8.13а) . (8.14)
. (8.14) . (8.15)
. (8.15)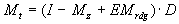 , (8.20)
, (8.20)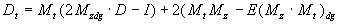 , (8.21)
, (8.21)


