Пример 8.1. Лесопосадки.
Допустим, что требуется оценить эффективность лесопосадочной операции и принять решение по ее повышению. В данном случае система включает лесопосадочную машину (ЛПМ) и набор саженцев (С), которые необходимовысадить на делянке с учетом требований технологии. В каждом шаге операции примем одну рабочую смену - 6 час. Предположим, что начало работы машины и подготовки саженцев происходит с одной и той же вероятностью p (причем отказ равен q=1-p). Очевидно, что после успешного начала работы ЛПМ могут произойти следующие случайные события: В1 - посадка всех саженцев произошла успешно и ЛПМ в конце работы исправна (цель операции достигнута); В2 - во время работы ЛПМ произошел отказ, который может быть устранен на месте (обычно время восстановления лимитируется 30 мин.); В3 - во время работы машины произошел неустранимый отказ и она должна быть заменена; В4 - при исправной работе машины из-за нарушения технологии посадка саженцев произведена некачественно и требуется пересев; В5 - из-за неисправной работы машины посадка произведена некачественно. Вероятность указанных условных событий (при условии успешного начала - p) обозначим:
а поскольку они несовместны и образуют полную группу, то
В результате реализации событий Вi [i=1,2,...,5] используемый процесс в любой момент времени может находиться в одном из следующих состояний А1 - посадка произведена успешно и в конце дня ЛПМ исправна; А2 - вследствие устранения отказа посадка произведена не пол-ностью. Исходя из допустимого времени устранения, можно полагать, что план не выполнен примерно на 15-20%; А3 - план не выполнен, требуется замена машины; А4 - план не выполнен, требуется новый комплект саженцев, ма-шина исправна; А5 - требуется новый комплект саженцев и исправная машина. Последнее состояние, по существу, является начальным. Если предположить, что состояние системы в начале каждого рабочего дня связано только с результатом предыдущего и вероятностным образом связано с ним то можно считать, что рассматриваемая операция представляет собой простую дискретную марковскую цепь. Кроме того, предположим, что переходные вероятности такой цепи не зависят от номера испытания (шага), то есть цепь является однородной. Из анализа состояний видно, что в состоянии А1 процесс останавливается (цель операции достигнута), т.е. оно является поглощающим. Таким образом, согласно принятым допущениям модель рассматриваемой операции представляет собой простую однородную поглощающую дискретную марковскую цепь с пятью состояниями. Переходные вероятности такой цепи определим с помощью алгебры событий:
А1 А2 А3 А4 А5
В соответствии с приведенным выше математическим аппаратом матрица (8.29) может быть представлена в каноническом виде:
где, в данном случае,
Подматрица Q, описывающая процесс переходов в системе до выхода из невозвратного множества состояний выделена двойным пунктиром в матрице (8.29). Как было сказано выше, после представления переходной матрицы в каноническом виде (8.29а), можно определить ряд характеристик, с помощью которых составляется целевая функция и принимается решение. В качестве критериев в данном случае могут фигурировать: 1. вероятность успешного проведения операции при заданном расходе средств на ее проведение Р(С2) - (прямая задача); 2. необходимое (гарантированное) количество средств, обеспечивающее проведение работы с заданной вероятностью; 3. математические ожидания и дисперсии случайных расходов средств на операцию. Рассмотрим в качестве критериев средние значения количеств ремонтов (или замен) ЛПХ - mz1 и комплектов саженцев mz2. Кроме того, в расходы войдут: стоимость частичного ремонта ЛПХ, а также расходы, связанные с дополнительным высевом саженцев при попадании в состояние А2. Таким образом, если задать величины расходов, связанные с попаданием в то или иное состояние (А2, А3, А4, А5) и опре-делить среднее число раз попадания в эти состояния, то в целом будут определены расходы на операцию. Представим таблицу (или матрицу) расходов в виде:
где Счр , Стр - соответственно, стоимость частичного или полного ремонта трактора; Сс - стоимость комплекта саженцев и их посадки. Среднее количество раз попадания в то или иное состояние (до поглощения) определится, как указывалось с помощью фундаментальной матрицы (стр.). При этом надо иметь в виду, что, поскольку в данном случае процесс начинается только с состояния А5 , то вычислять надо не все элементы матрицы (8.7), а лишь члены последней строки, т.е. m41, m42, m43 и m44. В буквенном выражении все элементы матрицы (8.7) представляют довольно сложные выражения, поэтому далее приведем конкретный числовой пример: Пусть значения ri будут равны: r1 = 0,77; r2 = 0,1; r3 = 0,05; r4 = 0,04; r5 = 0,03; р = 0,8. Тогда после вычислений матрица (8.7) будет иметь вид:
Тогда среднее число замен посадочного материала и трактора будет равно, соответственно: mс = m42 + m44 = 1,296; mтр = m43 + m44 = 1,375; а с учетом стоимости комплекта саженцев и материала: Се = 1,296 Сс + 1,375Стр (8.31) Полученное выражение (8.31) позволяет решить три задачи: 1. Определить, соответствуют ли расходы на операцию располагаемым; 2. Произвести выбор оптимальных значений ri , обеспечивающих min Се; 3. Оценить степень влияния каждой вероятности ri на эффек-тивность операции и наметить мероприятия по ее провышению.
Список Литературы. 1. Айзермана А. Элементы теории выбора – 2. Беляев И.П.,Трофимов Е.А. Системы поддержки принятия решений. -М.:ЦНИИ Электроника,1990 3. Гермейер Ю.Б. Игры с непротивоположными интересами. – М.: Наука, 1976. 4. Исследований операций в экономике. Учебное пособие. /Под ред. Н.Ш. Кремера. – М.:ЮНИТИ, 2006. - 407 с. 5. Катулев А.Н., Северцев Н.А. Исследование операций: принципы принятия решений и обеспечение безопасности, - М.: Физматлит, 2000. 6. Кини Р, Райфа Х. Принятие решений при многих критериях. М. Радио и связь, 1981 7. Козелецкий Ю.. Психологическая теория решений. М. Прогресс, 1979 8. Ларичев О.И. Наука и искусство принятия решений. М. Наука, 1979 9. Ларичев О.И. Теории и методы принятия решений, а также хроника событий в волшебных странах. Учебник. – М.: Логос, 2000. – 296 с. 10. Льюс Р. Д., Райфа Х. Игры и решения. 11. Мулен Г. Н. Теория игр с примерами из математической экономики. – М.: Мир, 1985. 12. Мулен Э. «Кооперативное принятия решений: аксиомы и модели». 13. Поспелов Г.С. Искусственный интеллект - основа новой информационной технологии,-М.:Наука,1988 14. Представление и использование знаний /Под ред.Уэно Х., Исидзука М. -М.:Мир,1989 15. Протасов И. Д. Теория игр и исследование операций. Учебное пособие /И.Д. Протасов.- М.: Гелиос АРВ, 2003.- 368с. 16. Таха Х. «Введении в исследование операций» 17. Уотермен Д. Руководство по экспертным системам. М.:Мир,1989 18. Черноморов Г.А. Теория принятия решений. Учебное пособие.- Новочеркасск: Электромеханика, 2002, 276 с. 19. Черноруцкий И.Г. Методы принятия решений: Учебное пособие. / И.Г. Черноруцкий.- СПб.: БХВ - Петербург, 2005 г. – 416 с. 20. Эддоуса М., Р. Стэнфилда. Теория принятия решений.
|

 ,
,  ; (8.27)
; (8.27)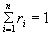 . (8.28)
. (8.28)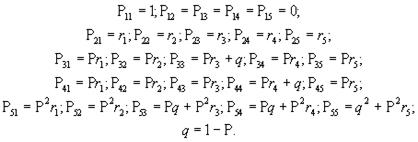 Соответственно, матрица перехода будет иметь вид:
Соответственно, матрица перехода будет иметь вид: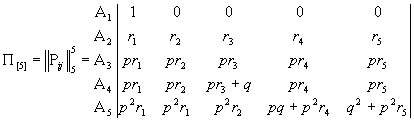 (8.29)
(8.29)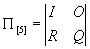 , (8.29а)
, (8.29а) - одноэлементная единичная под-матрица;
- одноэлементная единичная под-матрица; - нулевая вектор.строка;
- нулевая вектор.строка;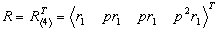 - вектор-столбец, описывающий переходы из невозвратных в эргодические состояния.
- вектор-столбец, описывающий переходы из невозвратных в эргодические состояния.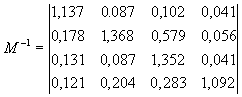 . (8.30)
. (8.30)


