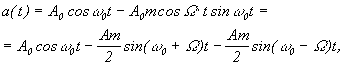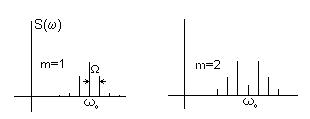Спектр радиосигнала при угловой модуляции частотной Итак, модулированное по углу колебание можно рассматривать как сумму двух амплитудно-модулированных колебаний (квадрупольных). Для определения спектра каждого из них достаточно сдвинуть на w0 спектр огибающих амплитуд, т. к. cosq(t) и sinq(t) являются нелинейными функциями своего аргумента q(t), то спектры этих функций могут существенно отличаться от спектра модулирующей функции s(t) и при однотональной модуляции возможно возникновение кратных и комбинированных частот. Однако при малых индексах модуляции т. е. Спектр, как и в случае амплитудной модуляции, состоит из несущей и двух боковых частей (но сдвинутых по фазе). При больших индексах модуляции за счет появления новых гармоник спектр расширяется и ширина спектра равна 2mW вместо 2W при m << 1. При m >1 cos(mcosWt) и sin (mcosWt) разлагают в ряд по Бесселевым функциям.
|
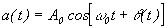. При фазовой модуляции 
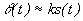, при
. Пр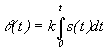еобразуем косинус суммы:,
.
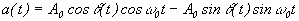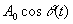и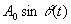 
- медленно изменяющиеся амплитуды.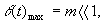
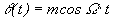можно положить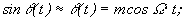 
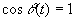, тогда
