Взаимно-корреляционная функцияДля оценки степени связи во времени между двумя различными сигналами
С другой стороны, согласно общей формуле определения спектральной плотности Положим в обеих формулах w = 0, получим: Итак, согласно общему интегральному представлению спектра сигнала спектральная плотность для ВКФ равна произведению спектральной плотности одной функции на сопряженную спектральную плотность другой. Автокорреляционная функция сигнала (АКФ) АКФ - это степень связи сигнала s(t) с его копией, сдвинутой на величину t.
При t = 0 получим равенство Парсеваля Итак, в частотной области имеется две характеристики сигнала: спектральная плотность и спектральная плотность энергии. Спектральной плотности Для периодических функций энергия бесконечна, поэтому автокорреляционная функция определяется путем усреднения по периоду: В более общем случае не обязательно периодического, но с бесконечной полной энергией сигнала принимают: Фурье образом такой автокорреляционной функции будет спектральная плотность мощности W(w), что видно из соотношения Однако практически спектральная плотность мощности определяется через функцию автокорреляции Пример. Автокорреляционная функция прямоугольного импульса
|
и 
используется взаимно-корреляционная функция ВКФ. 
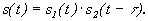Каждой из функций сомножителей соответствуют спектральные плотности 
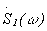и 
Согласно теореме о спектральной плотности произведения двух функций,
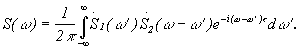
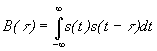, при t = 0 
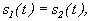
получим:
, 
.
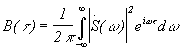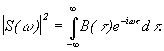
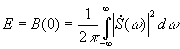, содержащей полную информацию о сигнале, соответствует в преобразовании Фурье сам сигнал s(t). Спектральной плотности энергии сигнала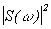 
, лишенной фазовой информации, в преобразовании Фурье соответствует автокорреляционная функция сигнала 
.
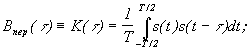
- средняя мощность сигнала.
.
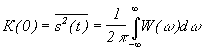. Формально 
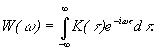
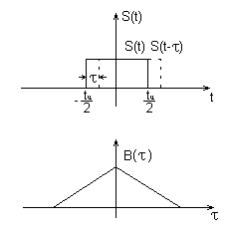
при 
