Балансная и однополосная амплитудные модуляции
В амплитудно-модулированном (АМ) сигнале: значительная доля мощности сосредоточена в несущем колебании
Однотональный АМ-сигнал с балансной модуляцией имеет вид: Такой сигнал с физической точки зрения является биением двух гармонических сигналов с одинаковыми амплитудами Другим усовершенствованием обычной амплитудной модуляции является удаление всех гармоник справа или слева от несущей частоты. При этом информация не теряется, так как содержится в оставшихся гармониках с другой стороны от несущей. Такая модуляция называется однополосной и позволяет в два раза сократить полосу занимаемых частот радиоканала, при этом существенно усложняется процесс демодуляции с полным восстановлением модулирующего сигнала. Возможно устранение в однополосной модуляции и несущего колебания с частотой w0.
Обобщенное представление радиосигнала в виде высокочастотного узкополосного колебания. Аналитический сигнал Используются радиосигналы, получаемые в результате одновременной модуляции амплитуды и угла где a1(t) - новая функция, связанная с исходной преобразованием Гильберта; Мгновенная частота узкополосного сигнала равна: Выделив в Из (1) следует, что в точках, где a1(t) = 0 имеем Следовательно, в этих точках кривые a(t) и A(t) имеют общие касательные. Кроме того, преобразование Гильберта обеспечивает в точках, где a1(t)=0, значения a(t), близкие к максимальным (амплитудным). Таким образом, функция A(t) касается функции a(t) в ее амплитудных значениях и ее можно считать простейшей огибающей, если она изменяется медленно по сравнению с быстро осциллирующей функцией a(t), т. е. выполнено условие узкополосного сигнала. Аналитическим представлением сигнала a(t) является комплексный сигнал Для спектральных плотностей функций a(t) и a1(t) имеют место соотношения Спектры аналитического сигнала имеют только положительные частоты. Корреляционная функция аналитического сигнала Пример. a(t) = cosw0t. Здесь использована замена t - t = x; Известно, что
|

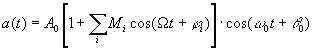
 Для более эффективного использования мощности передатчика можно формировать АМ-сигналы с подавленным несущим колебанием, реализуя так называемую балансную амплитудную модуляцию.
Для более эффективного использования мощности передатчика можно формировать АМ-сигналы с подавленным несущим колебанием, реализуя так называемую балансную амплитудную модуляцию.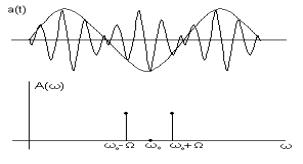
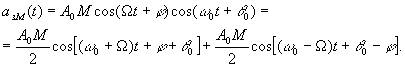

 и частотами
и частотами 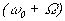 и
и 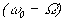 . При переходе огибающей биений через нуль фаза высокочастотного заполнения скачком изменяется на 180о, поскольку функция
. При переходе огибающей биений через нуль фаза высокочастотного заполнения скачком изменяется на 180о, поскольку функция 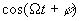 имеет разные знаки справа и слева от нуля. Осуществление балансной модуляции, как и обратного процесса демодуляции (детектирования), технически более сложно, чем при обычной амплитудной модуляции.
имеет разные знаки справа и слева от нуля. Осуществление балансной модуляции, как и обратного процесса демодуляции (детектирования), технически более сложно, чем при обычной амплитудной модуляции.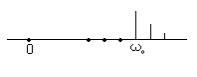
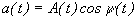 . При этом может возникнуть неоднозначность в выборе функций A(t), y(t) (можно A(t) представить в виде cos, а y(t) - в виде arccos и поменять местами). Однако если сигнал является узкополосным (ширина спектра модулирующих функций много меньше центральной частоты w0), то неопределенностей A(t) и y(t) можно избежать с помощью следующих соотношений:
. При этом может возникнуть неоднозначность в выборе функций A(t), y(t) (можно A(t) представить в виде cos, а y(t) - в виде arccos и поменять местами). Однако если сигнал является узкополосным (ширина спектра модулирующих функций много меньше центральной частоты w0), то неопределенностей A(t) и y(t) можно избежать с помощью следующих соотношений: ; (1)
; (1)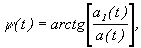 (2)
(2) ; (3)
; (3) (4)
(4)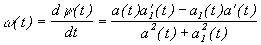 .
.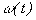 постоянную часть
постоянную часть  , можно написать
, можно написать 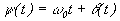 , где
, где 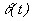 не содержит слагаемого, линейно зависящего от времени.
не содержит слагаемого, линейно зависящего от времени.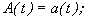
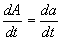 т. к.
т. к. 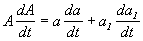 .
. где
где  - комплексная огибающая узкополосного сигнала.
- комплексная огибающая узкополосного сигнала. w > 0,
w > 0,
 w < 0,
w < 0, 
 связана с корреляционной функцией узкополосного сигнала
связана с корреляционной функцией узкополосного сигнала  соотношениями
соотношениями
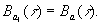
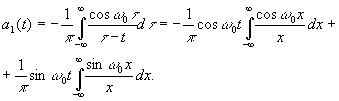

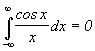 и
и 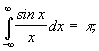 тогда
тогда
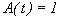 при
при 




