Случайные величины. , где p(x) - плотность вероятности, причем
Случайная величина описывается вероятностными законами. Вероятность того, что непрерывная величина х при измерении попадет в какой-либо интервал х1 <х <х2, определяется выражением: Моменты случайной величины: а) среднее значение (математическое ожидание) б) средний квадрат в) средний квадрат флуктуаций (дисперсия) Вид функции р(х) плотности вероятности для различных случайных величин может быть различен. Часто выполняется нормальный закон распределения вероятности: где Имеет место «центральная предельная теорема»: распределение вероятности для суммы независимых случайных величин с ростом числа слагаемых, при которых нет доминирующих, стремится к нормальному закону независимо от законов распределения слагаемых.
|
, где p(x) - плотность вероятности, причем 
. Для дискретной случайной величины хi P(x = xi)=Pi, где Pi - вероятность, соответствующая i-у уровню величины х. 
,
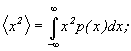
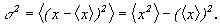
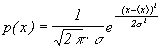- среднее значение, 
- дисперсия.
